Grounding internalism in the introduction process: from pop-gen to evo-devo
(work in progress: emerging manuscript, currently in the form of a persuasive essay)
Abstract
(This abstract is aspirational. The actual manuscript delivers the argument in a different way.)
Historical debates on evolution featured internalist ideas that were considered together with, or in opposition to, an externalist focus on natural selection. The mid-20th-century “Modern Synthesis” put an end to this kind of talk: internalist ideas were formally rejected, either for being incompatible with Mendelian population genetics, or merely for being unnecessary. Though internalist lines of thought re-emerged in the form of neo-structuralism and evo-devo, they are widely understood to evoke or require an alternative form of causation separate from population genetics. Here I explain why this impasse exists and how to remove it. First, I argue that an impasse on causation is genuine, and that it reflects how the received view of causation emerged from the distinctive boundary conditions and change-laws of a shifting-gene-frequencies paradigm in which the alleles relevant to evolution are already present in the initial gene pool, and causation is assigned (by an analogy with statistical physics) only to mass-action forces that shift their frequencies. Second, I describe a body of post-Synthesis theory that departs from this paradigm by representing the introduction of new alleles as a change-making process that is not a mass-action force. I show how an explicit treatment of the introduction of novelty by mutation-and-altered-development leads to direct contradictions with classic reasoning, most importantly the Haldane-Fisher “opposing pressures” argument that appeared to rule out evolutionary tendencies due to internal variational biases. Mutation-biased adaptation is a distinctive prediction of this theory, confirmed by recent empirical work. Third, I explain how this seemingly small modification to our understanding of causation represents a major innovation that allows us to specify a formal population-genetic grounding for the key internalist themes of (1) the evolutionary emergence of intrinsically likely forms, (2) internal taxon-specific dispositions that contribute to recurrent evolution; and (3) directional evolutionary trends that are internal in origin. Finally, I outline some of the initial successes and open challenges of a research program focused on the evolutionary impact of mutational, developmental, and systemic biases in the introduction of variation.
Introduction
An internalist-externalist distinction appears in many contexts. In the context of evolutionary thinking, externalist approaches focus on explaining the outcomes or products of evolution by reference to external conditions, so that, for instance, explanations for changes in some feature would make a linkage with changes in external conditions. Internalist approaches focus on explaining outcomes or products of evolution by reference to internal features so that, for instance, explanations for the emergence of some novel structure would be linked to intrinsic material or dynamic propensities of the evolving system. Internalists and externalists tend to differ not just in how they explain things, but in what they hope to explain: they typically are not just offering contrasting explanations for precisely the same things.
Contemporary internalism is manifested in neo-structuralist arguments about self-organization or findability in the manner of Kauffman (1993); in approaches to molecular evolution that feature mutational explanations (Cano, et al.); in the evolvability research front (Nuño de la Rosa), with its focus on how internal developmental-genetic organization facilitates evolution; and in evo-devo generally. Some of the classic internalist themes that persist into the contemporary literature are (1) the predominance (among the products of evolution) of forms or structures that are intrinsically or structurally likely, (2) taxon-specific evolutionary propensities or dispositions that contribute to recurrent evolution; (3) directional trends that are internal in origin.
For the present purposes, I will simplify this issue of internalism in the following way. Assume that evolution is fundamentally and essentially the result of combining a process of varigenesis, i.e., the generation of variation, and a process of reproductive sorting (resulting in selection and drift), and we are concerned only with the immediate or first-order implications of this combination. The internal factor in evolution is then primarily a matter of the genesis of variation, and the issue of internalism is primarily to understand the role of varigenesis in evolution, with a focus on how to combine variation and reproductive sorting. A key issue is whether varigenesis has a dispositional role, predictably favoring some types of changes or directions, and if so, how this dispositional influence operates, and how strongly it shapes evolution.
Before proceeding further, I want to note that this is a non-trivial simplification both conceptually and historically. For instance, the classic advocates of orthogenesis put their focus on how the genesis of variation influences evolution, but they were not strict internalists, e.g., some considered the environment as an important influence on the genesis of variation (see Ulett, 2014). Likewise, to equate internalism with the first-order effect of variation is to exclude higher-order ideas that figure importantly in internalist discussions, e.g., concepts of feedback through which evolvability evolves. My aim here is not to reduce all of evolution to one theory, nor even to cover all of the themes of internalism, but rather to provide a rigorous grounding for certain classic themes. To get to this point, I need to put some limits on the topic. Stated differently, this is an attempt at reduction or mechanistic justification— specifically an attempt to map certain pre-existing high-level themes to implications of a causal theory— and such reductive arguments typically shift the boundaries of things rather than perfectly mapping old themes to new mechanisms.
For my purposes here, “neo-Darwinism” refers to a view that posits specific and contrasting roles for selection and variation: selection is the potter and variation is the clay. In Darwin’s original theory, the process of indefinite variability (the noise-like environmental variation that Darwin relied on, later called fluctuation) merely supplies the raw materials that selection shapes into adaptations. Darwin said that variation follows immutable laws, but that these laws “bear no relation” to the structures built by natural selection. In this conception, variation is not dispositional. Selection is creative and imposes shape and direction, while variation merely supplies raw materials. In this view, “the ultimate source of explanation in biology is the principle of natural selection” (Ayala, 1970).
Although the neo-Darwinian combination of variation and selection— an unequal marriage in which one partner makes all the decisions and gets all the credit— has dominated evolutionary thinking, alternative views posit other roles for the process of variation, assigning it some leverage in influencing the course of evolution. A concise list of notional theories of the role of variation that have been most important in evolutionary discourse would look something like this, in chronological order:
- Variations emerge adaptively by effort, and are preserved, as per Lamarck
- Variation supplies in each generation the indefinite raw materials that selection shapes into adaptations, as per Darwin.
- The constrained generation of variation sets limits on the choices available to selection, as per Eimer (1898) or Oster and Alberch (1982)
- Mutation pressure drives alleles to prominence (against the opposing pressure of selection) under neutrality or high mutation rates, per Haldane (1927)
- New quantitative variation (M) contributes to standing variation (G) which, together with selection differentials (β), jointly determines (as Gβ) the short-term rate and direction of multivariate change in quantitative characters (Lande and Arnold, 1983; see note 5)
The first 3 theories are essentially folk theories, whereas the latter 2 are formalized. Theories of “orthogenesis” (perpetually mischaracterized by Darwin’s followers) from Eimer, Cope and others fall into the 3rd category, focusing on how the generation of variation influences evolution, and advocates of this kind of thinking considered both internal and external influences on the origin of variation (see Ulett, 2014).
The mutation pressure theory is explained below.
The formalization of evolutionary quantitative genetics (EQG) per Lande and Arnold (1983) is clearly an outgrowth of neo-Darwinian thinking, but the behavior of this formalism diverges significantly from selection and variation as the potter and the clay. The meaning of the master equation Δz = Gβ is that the trajectories of change for all variable traits are linked together (in a somewhat springy way) by their variational correlation structure, where G is the structured factor that represents the correlations in standing variation. However, G is standing variation, not varigenesis (M). Therefore the relation of selection and varigenesis in this theory is complex and indirect. See note 5 for more explanation.
Given how I have defined the problem of internalism in terms of the role of varigenesis, the issue of grounding internalism in causal theories is a matter of having a complete causal theory that specifies the kind of dispositional role of variation that makes sense of internalist themes.
In contemporary evolutionary discourse, there is clearly a discordance between the kinds of claims that internalist thinkers would like to support, and the kinds of claims with a vera causa status recognized by evolutionary geneticists. This discordance is reflected in (1) skepticism and dismissal from evolutionary geneticists, e.g., the way that Lynch (2007) dismisses basically all of evo-devo and the evolvability research front as speculation and loose talk, or the way that Wray, et al. (2014) refer to a “lack of evidence” for developmental bias, and likewise the way that Houle, et al (2017) take an attitude of extreme skepticism, denying that an influence of mutational variability on adaptation has been demonstrated in a way that fits with any known causal theory; and (2) the longstanding complaint from developmentalists about being left out of the “Synthesis,” which leads to the causal completeness argument (Amundson, 2005) and lineage explanation (Calcott, 2009), and to various calls for reform that emphasize the supposed limitations of population genetics.
Here I argue that we can specify a much broader and more complete grounding for internalism by adding (to the list above) a 6th theory about variation that is new and has not yet played a meaningful role in evolutionary discourse:
- Mutational and developmental biases in the introduction of variation impose kinetic biases on evolution by a first come, first served logic, without requiring neutrality or high mutation rates (Yampolsky and Stoltzfus, 2001)
To understand how to use this theory to specify a broad causal grounding for internalist concerns, we must remove a series of obstacles, beginning with a major historic error in the use of population-genetic reasoning — an error whose effects reverberate today — concerning a possible causal link between internal tendencies of variation and tendencies of evolution.
The Haldane-Fisher argument and the SGFT
Futuyma (1988) attributes 3 remarkable accomplishments to an “Evolutionary Synthesis” of the 20th century: re-establishing neo-Darwinism on a Mendelian basis, sweeping away all rival theories, and providing a common framework for scientists in various disciplines to address evolution.
How were rival theories rejected? In an argument repeatedly cited by leading thinkers, Haldane (1927) and later Fisher (1930) concluded that mutation is a weak force unable to overcome the opposing pressure of selection, important only when selection is absent or when mutation rates are abnormally high (for more detail, see here). The argument was understood to mean that, given the observed smallness of mutation rates (and the equally well recognized pervasiveness of selection on visible traits), internalist theories relating tendencies of evolution to tendencies of variation are incompatible with population genetics, e.g., Gould (2002) writes as follows, citing Fisher (1930):
“Since orthogenesis can only operate when mutation pressure becomes high enough to act as an agent of evolutionary change, empirical data on low mutation rates sound the death-knell of internalism.” (p. 510)
Gould (2002)
This is a formal argument with a clearly recognizable logic, the effect of which is to reject an entire class of internalist theories, with no need for difficult experiments or time-consuming analyses of data! Accordingly, Provine (1978), in “The role of mathematical population geneticists in the evolutionary synthesis of the 1930s and 1940s,” identifies this argument as a key theoretical claim (see also Stoltzfus, 2017, 2019).
“For mutations to dominate the trend of evolution it is thus necessary to postulate mutation rates immensely greater than those which are known to occur.” “The whole group of theories which ascribe to hypothetical physiological mechanisms, controlling the occurrence of mutations, a power of directing the course of evolution, must be set aside, once the blending theory of inheritance is abandoned. The sole surviving theory is that of Natural Selection” (Fisher, 1930)
“For no rate of hereditary change hitherto observed in nature would have any evolutionary effect in the teeth of even the slightest degree of adverse selection. Either mutation-rates many times higher than any as yet detected must be sometimes operative, or else the observed results can be far better accounted for by selection.” (p. 56 of Huxley, 1942)
“If ever it could have been thought that mutation is important in the control of evolution, it is impossible to think so now, for not only do we observe it to be so rare that it cannot compete with the forces of selection but we know this must inevitably be so.” (p. 361 of Ford, 1971)

But the argument is wrong.
An evolutionary process that depends on events of mutation that introduce new alleles is subject to biases in mutational introduction, by a first come, first served dynamic that Haldane and Fisher did not address in their arguments about mutation pressure (see note 8).
The flaw in the Haldane-Fisher argument arises from the assumption that evolution can be treated as a process of shifting the frequencies of alleles in an initial “gene pool,” without events of mutation that introduce new alleles. New mutations have to be involved somewhere in evolution, of course, but they don’t have to be directly involved: if all the relevant mutations happened in the past, and the corresponding variant alleles are present in the gene pool at frequencies resistant to random loss, then we don’t need to address new mutations to understand evolutionary dynamics, which would follow merely from shifting gene frequencies.
In this way, the shifting-gene-frequencies theory (SGFT) posits that evolution can be understood as a shift from an initial multi-locus distribution of allele frequencies, to a final distribution of frequencies for the same alleles. This is what “evolution is shifting gene frequencies” meant for modeling, in practice.
Note that this is a Newtonian framework for theorizing about dynamics. There is an initial state (a set of alleles with their initial frequencies), a set of boundary conditions (the frequencies may range between 0 and 1), and a set of change-laws that govern the dynamics, specifying how frequencies are shifted by mutation, selection, drift, migration and (in the multilocus context) recombination. Although the change-laws were often treated deterministically, stochastic versions also emerged.
Were the classic works of theoretical population genetics really built on thisnarrow foundation? Why isn’t this problem discussed more broadly? I’m not sure why this issue is not a primary focus of reformists, but certainly the issue has been noticed and remarked upon, and not just by non-conformists like myself or Nei (2014). Below are 3 independent sources authored by eminent evolutionary geneticists that note precisely this same restriction in classical theoretical population genetics:
“The process of adaptation occurs on two timescales. In the short term, natural selection merely sorts the variation already present in a population, whereas in the longer term genotypes quite different from any that were initially present evolve through the cumulation of new mutations. The first process is described by the mathematical theory of population genetics. However, this theory begins by defining a fixed set of genotypes and cannot provide a satisfactory analysis of the second process because it does not permit any genuinely new type to arise. ” (Yedid and Bell, 2002)
“Almost every theoretical model in population genetics can be classified into one of two major types. In one type of model, mutations with stipulated selective effects are assumed to be present in the population as an initial condition . . . The second major type of models [the origin-fixation type] does allow mutations to occur at random intervals of time, but the mutations are assumed to be selectively neutral or nearly neutral.” (Hartl and Taubes, 1998)
“We call short-term evolution the process by which natural selection, combined with reproduction . . ., changes the relative frequencies among a fixed set of genotypes, resulting in a stable equilibrium, a cycle, or even chaotic behavior. Long-term evolution is the process of trial and error whereby the mutations that occur are tested, and if successful, invade the population, renewing the process of short-term evolution toward a new stable equilibrium, cycle, or state of chaos.” (p. 182). “Since the time of Fisher, an implicit working assumption in the quantitative study of evolutionary dynamics is that qualitative laws governing long-term evolution can be extrapolated from results obtained for the short-term process. We maintain that this extrapolation is not accurate. The two processes are qualitatively different from each other.” (Eshel and Feldman, 2001, p. 163)
All three quotations suggest the same two things: (1) the SGFT was a limiting paradigm in mainstream 20th-century theoretical population-genetics, and (2) as the 20th century closed, this limiting paradigm was breaking down.
The breakdown started, perhaps, with origin-fixation models in 1969 (see McCandlish and Stoltzfus, 2014). For many years, these models were used primarily with neutral or slightly deleterious mutations: this explains the distinctive second category of Hartl and Taubes above. Eventually, SSWM models of adaptation (which overlap in meaning with origin-fixation models) emerged from Gillespie, and became the basis of the minor renaissance in modeling adaptation by Orr and others in the 1990s. That is, theoreticians have moved beyond the SGFT and embraced models of what is sometimes called the “lucky mutant” view or “mutation-driven” evolution, to such a degree that these models now represent a major branch of theory with diverse applications (see McCandlish and Stoltzfus, 2014; Tenaillon, 2014) (see note 9).
But the SGFT was influential in the past, and remains cryptically influential today. Michod (1981) identifies a shifting-gene-frequencies paradigm as the “hard core” of a research program per Lakatos:
(a) The Hard Core
The basic elements of Lakatos’s model are all clearly identifiable within the population genetics research programme. For the population geneticist, the common denominator of all evolutionary forces is their effects on gene frequencies. In other words, gene frequency changes are evolution. This proposition, the hard core of population genetics, is best summarised by Sewall Wright in the conclusion to volume II of his treatise (Wright [1969], p. 472):
“. . the species is thought of as located at a point in gene frequency space. Evolution consists of movement in this space.”
This point of view is the basis of the population genetics approach to evolution. This is as true today as it was during the synthesis of the 1920s and 30s.
Michod is correct to identify this as a paradigm, because of the way it defines a broad and powerful perspective on how to think about the problems of evolution, answering basic questions that otherwise might be very hard to answer, and which might be answered quite differently by scientists working on evolution from different perspectives:
- What is evolution? How do I know if it has happened?
- Where does evolution take place? What is the causal locale?
- How do I model evolution? What is the field or state-space?
- What are the causes of evolution? How do I quantify them and weigh their importance in evolution?
- How do I study evolutionary causes?
Certainly there were no agreed-upon answers to these questions prior to the Synthesis era. The distinctive answers suggested by the shifting-gene-frequencies paradigm shaped the Synthesis movement:
What is evolution? How do I know if it has happened? Evolution is shifting gene frequencies. Evolution has happened if there has been a shift in gene frequencies at the population level. A single event of birth or death is not evolution, and likewise, an event of mutation or recombination is not evolution. Instead, evolution has happened if there has been some significant shift in allele frequencies. We can argument ad nauseam about what “significant” means in this context, but this “how much X is enough?” question is trivial compared to the primary decision that X— the thing whose size we are going to argue about— is a shift in frequencies and not something else.
Where does evolution take place? Evolution takes place in populations because populations are cohesive entities with allele frequencies. Individuals do not have allele frequencies. Species have allele frequencies, but only because they exist as populations (one or more) with allele frequencies.
How do I model evolution? What is the field or state-space? As Wright (above) suggests, “the species is thought of as located at a point in gene frequency space. Evolution consists of movement in this space.” A model of evolution represents the evolving thing, the population, as a point moving in its state-space of allele frequencies under the action of the forces [10].
What are the causes of evolution? How do I quantify them and weigh their importance? The causes of evolution are the processes that cause shifts in allele frequencies, in units of frequency change over time. The forces that cause larger shifts are, by definition, stronger forces.
How do I study evolutionary causes? The only direct way to study evolutionary causes is to adopt the approach of population genetics, i.e., focusing on populations undergoing changes in allele frequencies, to assess what is causing those changes.
Some of the guidance provided by this paradigm turned into explicit dogma (e.g., the causes of evolution are forces that shift frequencies), and some of it was established more in the form of hidden assumptions or soft prejudices.
Considered more as a falsifiable claim than as a paradigm, the shifting-gene-frequencies theory asserts that we can understand evolution in nature adequately as a shift from one frequency distribution to another, so that any time-course of evolution can be represented as a trajectory in a continuous allele-frequency space.
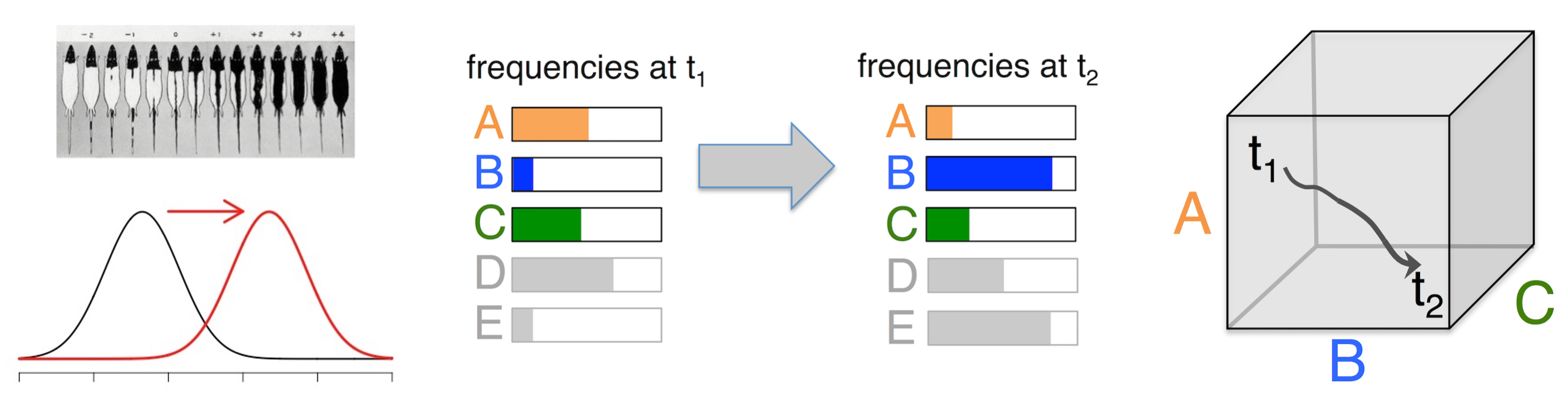
Within the SGFT, the forces of evolution are the biological processes that move the system in its state-space, i.e., the processes that shift frequencies. The ability to shift frequencies is obviously the measure of strength for a force: a biological process that causes larger shifts is necessarily a stronger force. Selection, being the strongest force, tends to dominate the process of shifting gene frequencies, i.e., it dominates the course of evolution.
What is the role of mutation in this theory?
In the process of shifting from an old to a new multi-locus frequency distribution, mutation pressure merely shifts the relative frequencies of pre-existing alleles. Because mutation rates are so small, these shifts are tiny in comparison to effects of selection and (typically) drift. Thus, the argument of Haldane and Fisher makes perfect sense within the SGFT.
That is, the Haldane-Fisher argument is both a fallacy (in a broader context) and, at the same time, the correctly derived implication of the SGFT: if evolution can be adequately understood merely as shifting gene frequencies, then mutation is indeed a weak force, unimportant unless selection is absent (neutral characters) or the rate of mutation is unusually large.

That is, mutation is a “weak force” in classical population-genetic thinking because the SGFT does not cover the novelty-introducing aspect of mutation. In effect, this aspect of mutation is treated as a background condition, rather than as a change-making causal process with explicit dynamics (see note 1). When a “gene pool” with pre-existing variation is assumed, the effect is that the novelty-introducing role of mutation is absorbed into this assumption as a background condition: the introduction process is literally is not part of “evolution” (shifting gene frequencies), but happens implicitly, before “evolution” gets started.
This theory makes mutation pressure largely irrelevant to modeling evolutionary change. This is why Lewontin (1974) says “There is virtually no qualitative or gross quantitative conclusion about the genetic structure of populations in deterministic theory that is sensitive to small values of migration, or any that depends on mutation rates.” The treatment of theoretical population genetics by Edwards (1977), shown in the image below, has hundreds of equations, but no terms for mutation. The word “mutation” appears only once in the entire book, on page 3, where the author says “All genes will be assumed stable, and mutation will not be taken into account.”

Note that the SGFT does not imply or suggest that new mutations never happen. Haldane, Dobzhansky and others stated explicitly that evolution ultimately would grind to a halt without new mutations. Instead, the verbal theory of the SGFT says that, even though mutations are ultimately necessary, they are not immediately necessary, i.e., they are not directly involved, because the “gene pool” acts as a dynamic buffer, maintaining variation so that there is always abundant material for selection to respond to a change in conditions.
The popularity of the SGFT was driven partly by the sense that adaptation would be too slow if it involved waiting for the right mutation, instead of beginning with an abundant gene pool (e.g., this is particularly emphasized in Wright’s 1932 paper). Before about 1940, when the age of the earth was established at 4000 MY instead of 20 MY or 200 MY, evolutionary biologists were particularly motivated by the need to establish that the process of evolutionary adaptation was fast enough to explain observed levels of adaptation and diversity. We don’t think like this anymore, but a century ago, a theory of evolution that made adaptation fast was considered to be ex posteriori a better theory.
In addition, the SGFT was experimentally validated, a known mechanism. The experimental touchstone for the SGFT was Castle’s famous experiment with hooded rats (see Provine, 1971). Johannsen had already proven that selection is effective in sorting out true-breeding Mendelian types, but Castle and his colleagues showed something quite different. They started with a population of mottled black-and-white rats, and bred nearly all white, and nearly all black populations by selection in just 20 generations, not enough time for new mutations to play any appreciable role. This proved that selection could create “new types” (Provine) or “wholly new grades” (Castle) without the involvement of mutation, simply by shifting gene frequencies.
Finally, the SGFT provided a rhetorical foundation for Darwin’s followers to reject mutationism in the sense of “mutation proposes, selection disposes” (decides), a non-Darwinian theory distinct from their gradualist conception of evolution by the shifting and blending of abundant infinitesimals. The mutationist conception of evolution as a 2-step mutation-fixation process — the “lucky mutant” theory formalized in 1969 in origin-fixation models — is common today (see The shift to mutationism is documented in our language). However, the architects of the Modern Synthesis called on the SGFT to argue against the lucky mutant view (for more detail, see When Darwinian Adaptation is neither). That is, even though the SGFT was a speculative theory of unknown realism, the architects of the Modern Synthesis convinced themselves that the theory was firmly established, and they conveyed this attitude of certainty to their readers, e.g.,
“Novelty does not arise because of unique mutations or other genetic changes that appear spontaneously and randomly in populations, regardless of their environment. Selection pressure for it is generated by the appearance of novel challenges presented by the environment and by the ability of certain populations to meet such challenges.” (Stebbins, 1982, p. 160)
“It is most important to clear up first some misconceptions still held by a few, not familiar with modern genetics: (1) Evolution is not primarily a genetic event. Mutation merely supplies the gene pool with genetic variation; it is selection that induces evolutionary change.” (p. 613 of Mayr, 1963)
This commitment continued to echo for decades in the notion that evolution does not depend on new mutations, a doctrine repeated in textbooks, e.g.,
“In practically all populations, however, the role of new mutations is not of immediate significance” (p. 464)
Strickberger MW. 1990. Evolution. Boston: Jones and Bartlett Publishers.
Thus, the SGFT was not merely a modeling convention — it was not just a technique used by mathematicians to make the equations easy to solve. Instead, the formal models and the conception of forces as mass-action pressures came together with a verbal theory about how evolution actually works in nature, and this integrated theory provided a basis to reject, not just orthogenesis, but mutationism in the sense of evolution via new mutations, i.e., mutation proposes, selection disposes (decides).
Even more broadly, the SGFT underlies the grand Synthesis claims noted earlier (Futuyma, 1988): restoring neo-Darwinism, sweeping away all rivals, and providing a unified framework for scientists in various disciplines to address evolution.
Yet, evolution in nature does not have to follow the SGFT. As stated earlier, an evolutionary process that depends on events of introduction — events of mutation that introduce a new allele, or events of mutation-and-altered-development that introduce a new phenotype — is subject to biases in the introduction process, by a simple “first come, first served” logic.
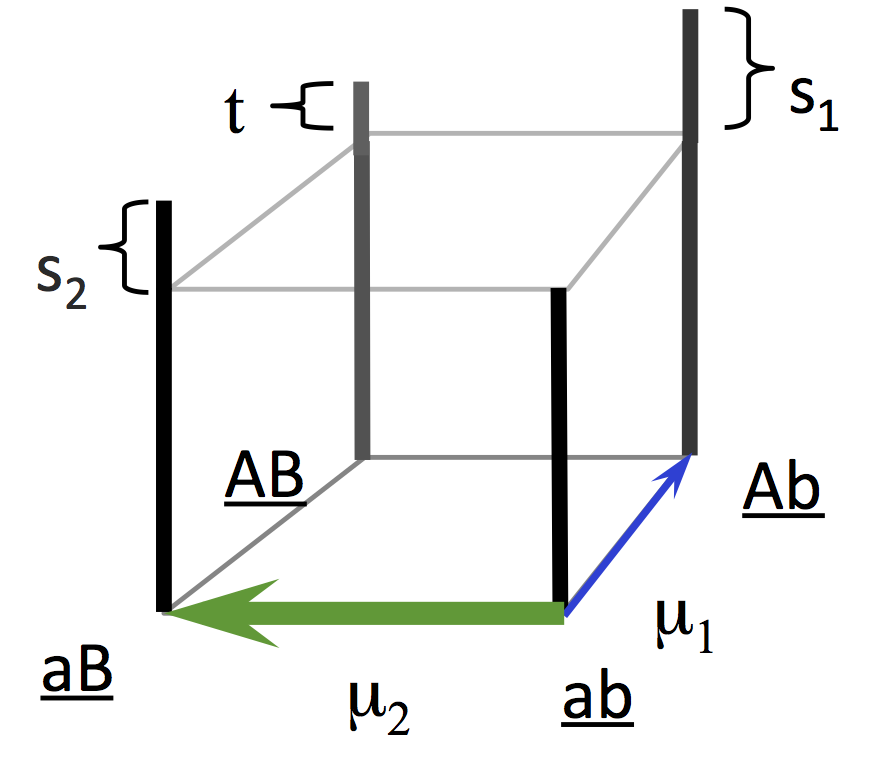
The logic of this theory was demonstrated by Yampolsky and Stoltzfus (2001) using a population-genetic model with 2 loci and 2 alleles. From the starting ab population, mutations with rates u1 and u2 introduce the beneficial genotypes Ab or aB, with a mutation bias favoring aB with magnitude B = u2 / u1 and with a greater fitness advantage (here, 2-fold) favoring Ab. The lines in the plot below all go up from left to right, indicating that the bias in outcomes (frequency of evolving aB relative to Ab) increases with the bias in mutation. The smaller populations show the degree of bias expected under origin-fixation dynamics (dashed line).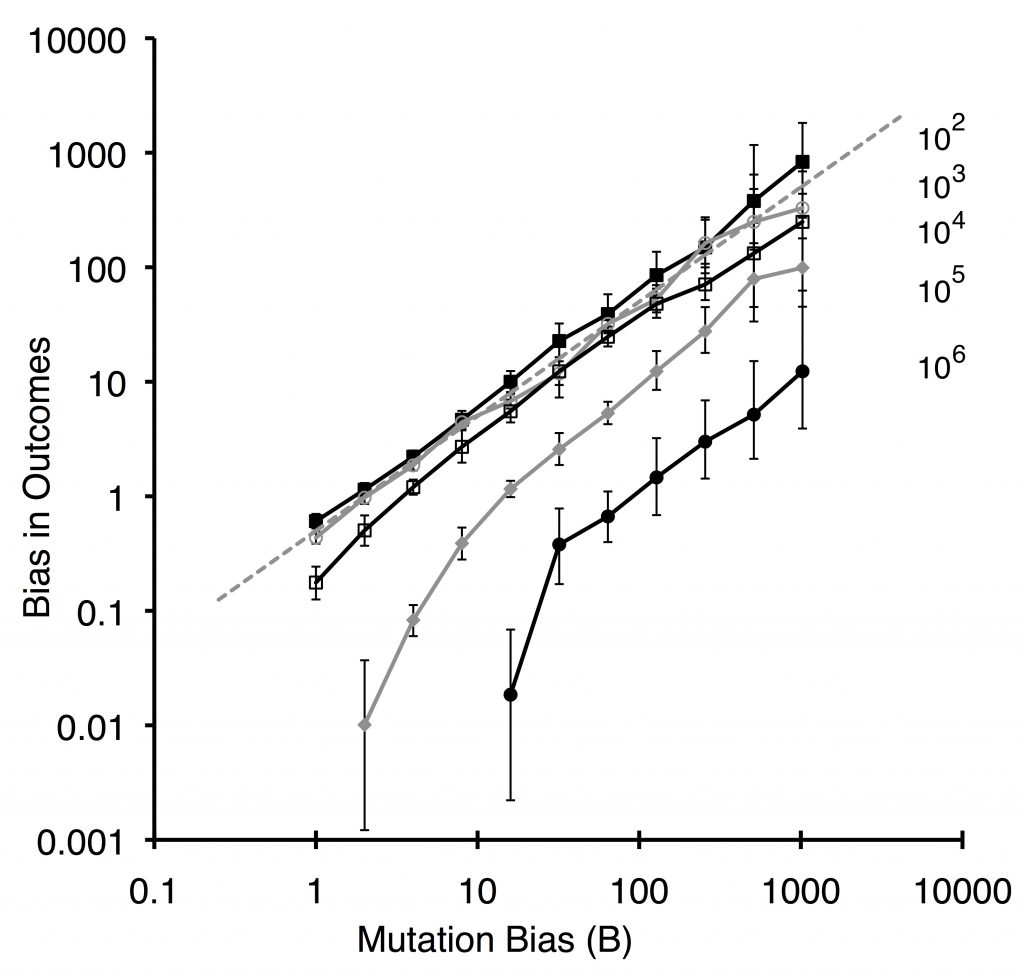
A distinctive prediction of this theory is that the influence of mutation biases does not require neutrality or high mutation rates (contra Haldane 1927), but will emerge (under the right conditions) from biases in ordinary types of nucleotide mutations, e.g., transition-transversion bias. This effect has been demonstrated conclusively in the past few years in both laboratory adaptation and in cases of natural adaptation (in diverse taxa) traced to the molecular level (for review, see Gomez, et al. 2020 or Stoltzfus, 2019).
Thus, a causal link between tendencies of variation and tendencies of evolution is theoretically possible and is actually observed. This result refutes a key argument from the mid-20th-century orthodoxy: internalist theories that attempt to link evolutionary tendencies to internal tendencies of variation are not inherently incompatible with Mendelian population genetics, but only with the SGFT (see note 2).
Repercussions
So far, we have established that the Haldane-Fisher argument is unsound theoretically, and that its conclusion is contradicted empirically. Haldane’s (1927) conclusion, even when considered narrowly, does not provide correct guidance for reasoning about evolution, e.g., when we see mutational patterns in molecular evolution, we cannot assume that this must reflect high mutation rates or neutral evolution. And the broad application of the Haldane-Fisher argument as a cudgel against internalism is crazy wrong.
Yet, in regard to the structure of evolutionary thought, much intellectual work will be required to reverse the damage done by this influential fallacy. Evolutionary discourse has proceeded through a century of theory development and exploratory thinking subject to the constraints that (1) a workable theory of biases in the introduction process was unknown to its major participants, and (2) the Haldane-Fisher argument placed a large “Do Not Enter” sign on the door leading to internalist thinking. This is a disturbing thought.
This limitation was not known, for instance, in the 1980s, when the Modern Synthesis was being challenged on various fronts (molecular evolution, macroevolution, evo-devo), and reformers were exploring new ways of thinking. Gould and Lewontin did not know it in 1979, when they wrote their famous critique of adaptationist thinking. Maynard Smith, et al. did not know it in 1985 when they wrote about “developmental constraints.” Kauffman did not know it in 1993 when, in The Origins of Order, he invoked “self-organization” to explain the findability of structures that are common in genetic state-spaces.
Yet all 3 sources are widely cited and have been influential — evidence of widespread hunger for internalist or structuralist alternatives to neo-Darwinism.
What happened, and what didn’t happen, because of this “do not enter” sign?
In the “spandrels” paper, Gould and Lewontin (1979) eviscerated the adaptationist research program, but their arguments for alternatives to natural selection were unconvincing. Twenty years later, at the close of his career, Gould (2002) cited the Haldane-Fisher argument and wrote (as quoted above) that “empirical data on low mutation rates sound the death-knell of internalism” (p. 510). What if Gould had known all along that this argument is mistaken?
Maynard Smith, et al. (1985), in their seminal piece on “developmental constraints,” noted explicitly that the Haldane-Fisher argument posed a barrier to the proposed efficacy of developmental biases in variation. If a theory of biases in the introduction process had existed in 1985, Maynard Smith, et al. could have used it to refute the Haldane-Fisher argument, and to justify their claims regarding developmental effects, yet their foundational statement offers no general answer to the crucial problem of lacking a valid population-genetic basis (in the highlighted passage, they go on to suggest neutral evolution, obviously not an adequate foundation to address evo-devo concerns).


Accordingly, Reeve and Sherman (1993), in their subsequent defense of the adaptationist program, cited Gould and Lewontin as well as Maynard Smith, et al. (1985) and complained that the advocates of developmental constraint had offered no evolutionary mechanism. They called on the logic of the Haldane-Fisher argument when they ask, rhetorically, “why couldn’t selection suppress an ‘easily generated physicochemical process’ if the latter were disfavored?” Decades later, the notion of developmental constraint remains a flexible explanatory concept not tied to a specific evolutionary mechanism (see Green and Jones, 2016).
In the discourse of developmentalists, the lack of a population-genetic mechanism for this effect has led to an exploration of alternative views of causation. That is, developmentalist-structuralist thinkers ignored the “do not enter” sign and continued to assume that internal factors actually matter in evolution. Yet, because classical population genetics did not seem to provide a causal basis for this intuition, they concluded that population genetics has some kind of metaphysical limitation that makes it inadequate as the basis for complete causal theories.
That is, due to the influence of the SGF paradigm, population genetics is widely accepted as the language of causation in evolution, e.g., Dobzhansky (1937) declared that “Since evolution is a change in the genetic composition of populations, the mechanisms of evolution constitute problems of population genetics.” Yet, by the Haldane-Fisher argument, population-genetics rules out a dispositional role for internal variational factors. This has led internalist thinkers to suspect that something about population genetics makes it inadequate to construct complete accounts of evolutionary change.
“intellectually respectable evolutionary theorizing must be based on population genetics theory, which forms the substantive core of the relevant evolutionary theory.”
Sarkar (2014)
The causal completeness argument (Amundson, 2001, 2005) is a formalization of this complaint against population genetics. Because phenotypes exist and they are the stuff of evolution, an account of evolutionary causation that refers only to population genetics cannot be complete: development must fit in, somewhere, in a causal role. One way to integrate this role is to suggest that a full account of evolution must combine (1) the usual dry population-genetic account of causation by forces with (2) an alternative narrative of wet biological changes in development (e.g., Wilkins, 1998). This completes the causal account of evolution by supplementing standard forces with a kind of “lineage explanation” per Calcott (2009). In lineage explanation, the focus is on constructing a developmental-genetically plausible narrative for changes in a lineage over evolutionary time, as opposed to a focus on individual development over a lifetime, or on population genetics over evolutionary time.
The problem of a missing causal foundation manifests differently in the (completely separate) literature of molecular evolvability or self-organization following on Kauffman (1993). Kauffman sought to explain why certain features or forms emerge commonly by evolutionary processes, even without being selected.

A possible causal explanation emerges from the fact that the structures that are more common in genetic state-space, e.g., RNA folds that have more possible sequences, necessarily have more mutational arrows pointed at them, including from other parts of state-space.
We might be tempted to suggest that this fact alone explains the findability of common structures, but this only tells us that a mutational bias exists — how such a bias influences evolution is a separate issue that requires a population-genetic theory linking tendencies of mutation to tendencies of evolution.
To grasp this point more clearly, think of Sober’s (1984) distinction of “source laws” and “consequence laws” of selection. Population genetics tells us how to compute what will happen in a population if A and B differ in fitness by some amount such as 2 %, given some background conditions including a scheme of heredity. That is, population genetics covers the consequence laws of selection. But it doesn’t tell where the differences in fitness come from, i.e., how they emerge biologically. For that, we need the source laws of selection, which come from physiology and ecology and so on.
Likewise, a complete causal theory for a variational influence would require both source laws that address how the variational tendencies emerge, and consequence laws that address their impact on evolution. As noted above, Maynard Smith, et al. (1985) drew attention to the source laws for developmental tendencies of variation, but failed to supply a consequence law linking those to measurable evolutionary effects.
More generally, in the evo-devo literature, the focus is on developmental source laws, and the issue of consequence laws is often not identifiable (e.g., Salazar-Ciudad, 2021), so that the assumption that tendencies of variation must somehow cause evolutionary tendencies is wholly implicit.
By contrast, for more traditionally minded evolutionary geneticists, the issue raised by evo-devo is precisely this alleged causal link between developmental biases and evolutionary ones, a link that is considered problematic and unlikely. For instance, in “Mutation predicts 40 million years of fly wing evolution,” Houle, et al. (2017) have done perhaps the finest and most rigorous work to date showing a detailed quantitative correlation between (1) measured tendencies of varigenesis, i.e., new phenotypic variation M, and (2) measured patterns of evolutionary divergence R. This seemed to resolve 40 years of debate over the evo-devo claim that developmental biases influence evolution, an argument that was always based far too much on developmental models of variation, instead of actual measurements of mutational variability. But the authors themselves take an attitude of utmost skepticism and deny that their results demonstrate a causal link from M to R.
When we are considering discrete traits, the Haldane-Fisher argument provides the consequence laws for biases in variation under the SGFT. Mutation is a weak force because mutation rates are small. Therefore, tendencies of mutation cannot be difference-makers in evolution, except in the case of neutral characters or unusually high mutation rates (Haldane, 1927).
Today, however, we can reject the SGFT and the Haldane-Fisher argument, and instead invoke the mutationist dynamics of origin-fixation models (for instance) to propose that the joint probability of origin-and-fixation of common structures (i.e., common in abstract genotype-spaces) is higher because their probability of mutational origin is higher. In this way, we can specify a complete chain of causation linking (1) a source law specifying that common structures have more mutational arrows pointed at them, with (2) a consequence law specifying that biases in the mutational introduction of alternative structures impose a bias on evolution (dependent on population-genetic conditions). Note that the consequence law comes from population genetics but the source law does not: it comes from a model for how RNAs develop a phenotype (i.e., how they fold into a shape), and then mapping the phenotypes (shapes) to genotype space.
But this kind of reasoning did not exist in 1993, and few scientists know about it today. Thus, proponents of effects of findability describe it in other ways, e.g., Kauffman invoked “self-organization.” The general response of evolutionary geneticists to Kauffman’s work was that he clearly had some fascinating results, but it was not clear how relevant they were (given the abstractness of the models), or what they said about evolutionary causes. Kauffman repeatedly said that selection and “self-organization” worked together, in a partnership. But Kauffman was not calling on the usual list of evolutionary forces that shift allele frequencies to give a mechanistic account of self-organization, so we had no way to evaluate the causal status of this partnership. One reviewer called his references to self-organization “almost magical” (Fox, 1993).
In other parts of the contemporary literature on molecular evolvability, the effects of proximity and cardinality (of connected phenotype networks in genotype-space) that, in the above interpretation, are mediated by biases in the introduction process, are described as an effect of background conditions, as “constraints” emerging from properties of fitness landscapes (e.g., here), rather than being described in terms of causal forces.
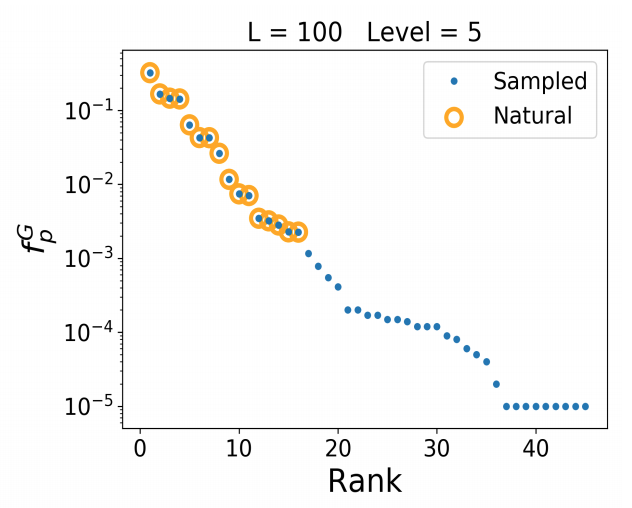
In this way, the findability phenomenon is presented as something related to the complexity of the space in which evolution happens, i.e., patterns emerge, not due to any particular evolutionary force, but due to the unavoidable geography of the state-space for evolution. Yet the dependence of findability on the way that this state-space is sampled by mutation, leading to biases in the introduction process (Stoltzfus, 2012), is shown by Schaaper and Louis (2014). They refer to this effect as the “arrival of the frequent” or as “phenotype bias.” Likewise, Dingle, et al (2020) show that the findability effect disappears when sampling compensates for the differing cardinality of structures in sequence space.
A causal grounding for internalism
“What the world most needs, then, is not a good five-cent cigar, but a workable — and correct — theory of orthogenesis.”
(Shull, 1935)
Thus, the central barrier to establishing a causal grounding for internalist thinking in evolutionary biology is that the prevailing theory of causal forces is grounded specifically in a limited conception of evolutionary genetics (the SGF paradigm), rather than in a more general conception that implicates events of introduction. A more general conception of causation would include causes that are not formally population-genetic forces.
What are the classical forces? In the conception of causation grounded in the SGFT, a causal force is a mass-action pressure modeled after the pressures of statistical physics, i.e., a pressure is a pressure on allele frequencies, and it results from aggregating over the effects of innumerable events among the individual member organisms of a population (see Sober, 1984). Selection and drift result from the aggregate effects of innumerable births and deaths. The force of mutation is mutation pressure, the aggregate effect of innumerable events of mutational conversion in different individuals.
Note that, just as statistical physics is not a reductionist theory, the SGFT is simply not a reductionist theory, in the sense of pushing the fundamental basis of reality or causation down to the lowest possible level. The SGFT clearly posits an emergent population “level”, and the architects of the Modern Synthesis argued explicitly that the forces of evolution are emergent at the population level, and do not exist at the more reduced level of individual organisms. For instance, in their textbook, Dobzhansky, et al (1977) write
Each unitary random variation is therefore of little consequence, and may be compared to random movements of molecules within a gas or liquid. Directional movements of air or water can be produced only by forces that act at a much broader level than the movements of individual molecules, e.g., differences in air pressure, which produce wind, or differences in slope, which produce stream currents. In an analogous fashion, the directional force of evolution, natural selection, acts on the basis of conditions existing at the broad level of the environment as it affects populations. (p. 6)
The correct association of the concept of reduction, in regard to the role of population genetics in the Modern Synthesis, has to do with theory reduction. The Modern Synthesis clearly takes a set of recognized high-level phenomena of evolution, primarily the phenomenon of adaptation, and attributes them to the consequences of a set of underlying causal processes. The phenomenology is reduced to the operation of causes in this way.
The particular conception of an emergent population force (in the SGFT) means that an individual event of mutation that introduces a new allele does not satisfy the definition of an evolutionary cause. It is a proximate cause, in the language of Mayr. Likewise, the development of an individual is a proximate cause.
A casual way to state the consequences of this limitation is that the prevailing theory of causal forces used in evolutionary reasoning works well for causes of fixation but not for causes of origination, yet a full account of evolutionary causation requires that both origination and fixation are treated as change-making causal processes with explicit dynamics.
Thus, the flaw in the forces theory is exactly the same thing as the flaw in the SGFT. The sufficiency of the SGFT depends on evolution remaining in the topological interior of the relevant allele-frequency space, where all frequencies are non-zero. In this topological interior, all of the classical forces are identical in the sense that each force can change a frequency f to f + δ, where δ is an infinitesimal. A change from f = 0.5000 to 0.5001 can happen by any force, although a shift of 1 part in 5,000 is a large shift for mutation because mutation rates are so small. A process that causes larger shifts is a stronger force. Mutation is a very weak force.
In this way, the scheme of “forces” achieves generality by a common currency of causation, infinitesimal mass-action shifts in frequency. In the interior of the state-space for evolution (in the SGFT), any infinitesimal change, anywhere in the space, can happen by any force. This means that we can chain together any series of infinitesimal changes into a trajectory, and this trajectory can (in principle) be caused by any force, or by any combination of forces.
But the logic of forces falls apart if we consider movement from the surface (edge) of an allele-frequency space into the interior. In the left figure below, we have a small shift from the center of a 2-dimensional allele-frequency space (0.5000, 0.5000) to (0.5002, 0.5004). This could be caused by selection, drift or mutation, or by any combination of them, although again, a shift this large is enormous for mutation alone, and would not normally happen in one or a few generations. In the right figure, this same change in frequencies is moved down to the horizontal axis, i.e., the shift is now from (0.5000, 0) to (0.5002, 0.0005). This is the same shift mathematically, but not evolutionarily, because mutation is absolutely required to cause a shift upward from 0.
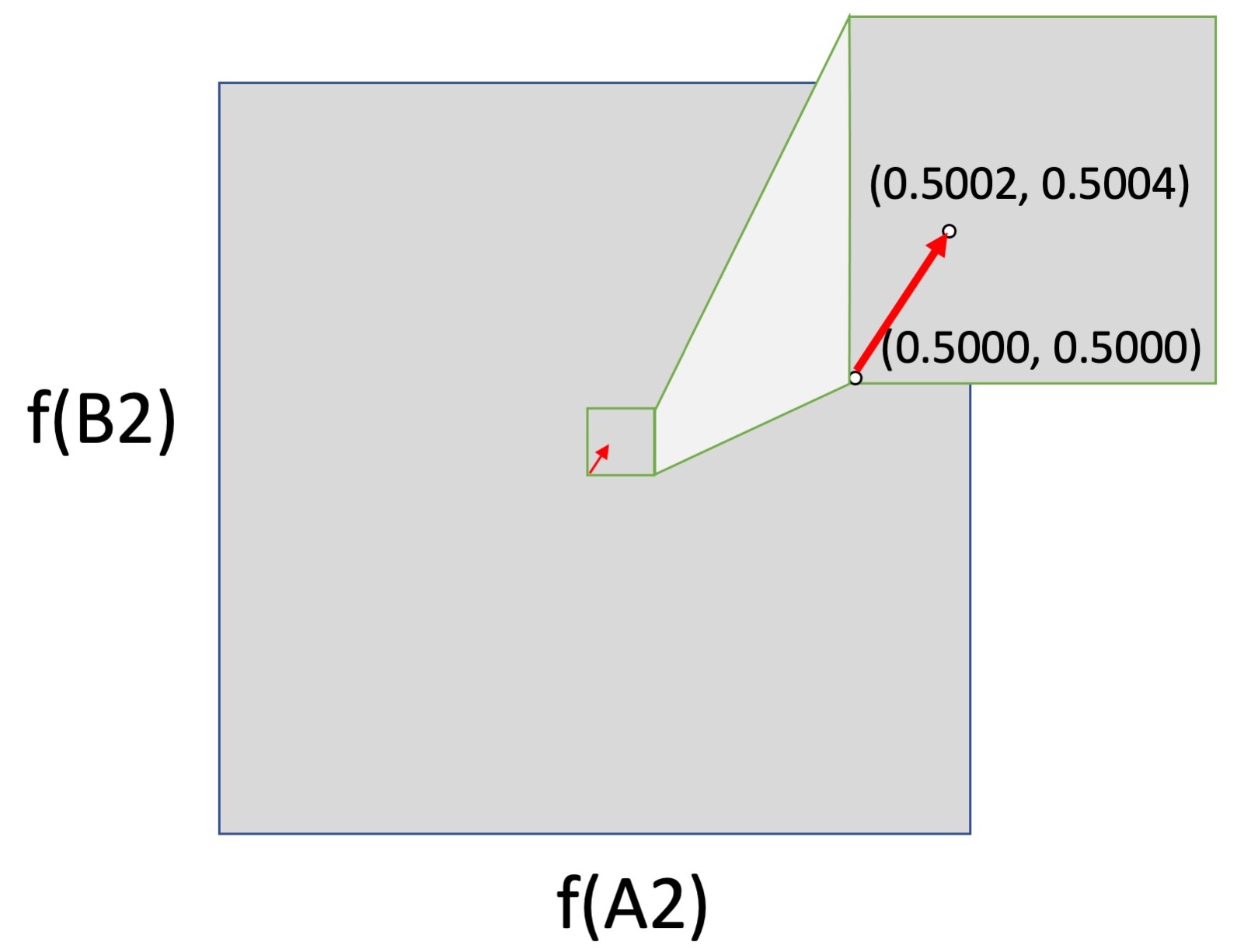
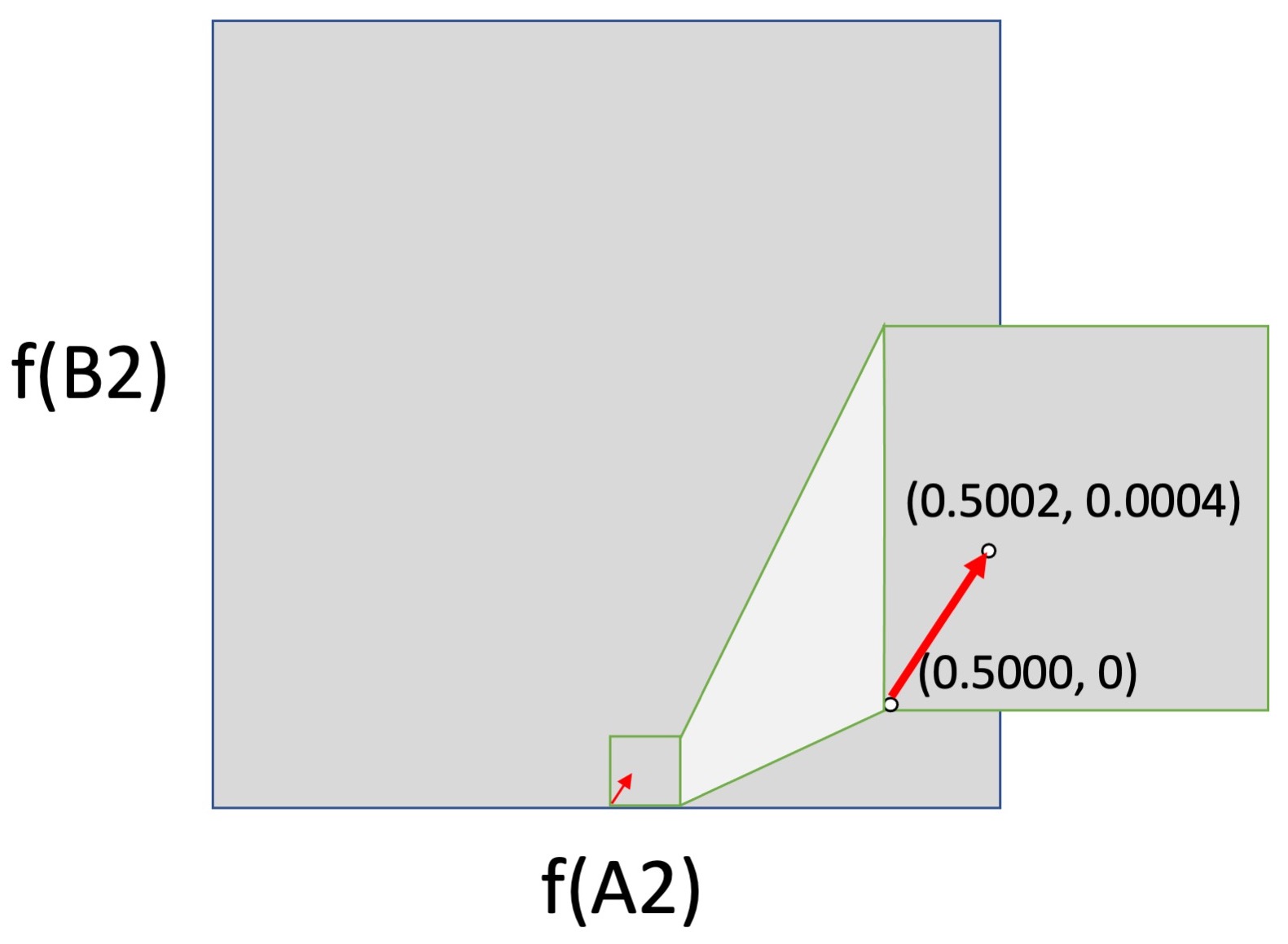
The logic of forces breaks down because the impact of the biological process of mutation is weaker than every other force in the interior of an allele-frequency space, but infinitely stronger than every other force at the surfaces, where it acts by discrete events, not continuous shifts. This is qualitatively different causal behavior. When an evolutionary process includes discrete events of introduction that jump an evolving system off of the surface of an allele-frequency space into the interior (where the forces of selection and drift operate), mass-action pressures are not a sufficient guide to causation.
This argument might sound very abstract, thus not relevant to practical evolutionary reasoning. Yet, anyone who saw how the evo-devo challenge played out in the 1980s and 1990s knows that abstract arguments about what qualifies as a true evolutionary cause (i.e, not development) have been deployed with great effect against claims of novelty from evo-devo. For instance, Wallace (1986) asks whether embryologists can contribute to understanding evolutionary mechanisms, and then answers negatively, arguing that “problems concerned with the orderly development of the individual are unrelated to those of the evolution of organisms through time.”
“If we are to understand evolution, we must remember that it is a process which occurs in populations, not in individuals. Individual animals may dig, swim, climb or gallop, and they also develop, but they do not evolve. To attempt an explanation of evolution in terms of the development of individuals is to commit precisely that error of misplaced reductionism of which geneticists are sometimes accused” (Maynard Smith, 1983, p. 45).
“I must have read in the last two years, four or five papers and one book on development and evolution. Now development, the decoding of the genetic program, is clearly a matter of proximate causations. Evolution, equally clearly, is a matter of evolutionary causations. And yet, in all these papers and that book, the two kinds of causations were hopelessly mixed up.” (Mayr, 1994)
“No principle of population genetics has been overturned by an observation in molecular, cellular, or developmental biology, nor has any novel mechanism of evolution been revealed by such fields.” (Lynch, 2007)
To escape this kind of smack-down from powerful scientists whose judgments continue to guide the field, presumptive causal arguments from evo-devo, or from any other sub-field in evolutionary biology, must refer to the forces of population genetics, because the statistical forces theory is the only accepted theory for what constitutes a genuine evolutionary cause.
But if events of introduction are evolutionary causes, and biases in the introduction process are causes of evolutionary bias, then
- events of mutation can be evolutionary causes,
- events of mutation-and-altered-development that introduce new phenotypes can be evolutionary causes, and
- mutational and developmental biases in the generation of variation can be evolutionary causes.
In particular, when the introduction process is recognized as causal, this allows us to specify a formal locale of causation in which to recast the plausibility arguments in lineage explanation into arguments about the developmental factors that induce biases in the introduction process.
That is, this kind of causal grounding for internalist thinking does not repudiate the familiar elements of population genetics or supplement them with a parallel plane of developmental causation, but instead is based on (1) pointing to the part of mathematical theory covering the introduction process, which already exists and is currently in active development, (2) taking into account what we now know about the powerful influence of this qualitatively distinct process on the observed course of evolution, and the theoretically expected course, and finally (3) insisting that we must locate a cause in this part of population genetics, i.e., we must declare that the introduction (origination) process is a genuine cause, a change-making causal process with propensities that must be treated explicitly (again, see note 2).
To be perfectly clear, the necessity of doing this, justifying the use of “must” in the previous paragraph, is that the evidence (see Payne, et al 2022, Gomez, et al. 2020 or Stoltzfus, 2019) compels us to recognize that the dynamics of mutational introduction are profoundly consequential, and our theorizing suggests that a far broader role is inevitable. The notion that we can treat evolution as shifting gene frequencies, without directly involving the dynamics of introduction, is untenable, and the required correction to our conception of causation is to recognize the introduction process (mutational or otherwise) as something that must be treated explicitly as a cause in order to get evolution right.
To the extent that the term “population genetics” is associated with the SGF paradigm of the population as a cohesive emergent entity subject to causal displacement only via the classical mass-action forces, this expanded framework to account for evolutionary change is not population genetics because it breaks the SGF paradigm, i.e., we could choose to avoid the term “population genetics” and use a broader term like “evolutionary genetics.” However, this is just a question of labels. What is important to understand is that, regardless of the labels, we are breaking historical precedent and departing from the SGF paradigm in a way that induces new rules: integrating the introduction process induces qualitatively different behavior that explicitly contradicts the implications of population-genetic causation as it was understood (for instance) by Haldane and Fisher.
[The last 3 paragraphs are worth re-reading. ]
From the beginning, critics of Darwin’s thinking have objected that selection does not create anything new, and that the theory is therefore missing something fundamental. Darwin’s followers developed several well known responses to this objection, justifying the creativity of selection (see Ch. 6 of Stoltzfus, 2021). One of them is essentially that there is infinitesimal variation in every trait, and selection can leverage that diversity to create novelty solely by quantitative shifts. In a world consisting of a fixed set of continuous quantities (e.g., quantitative genetics), this is abstractly true. Another response is that selection is creative in the sense of bringing together rare combinations out of the diversity of the gene pool. This is also true, in a sense that depends on presuming mechanisms of recombination. Another argument is that selection can accrue effects in a particular direction, consistently, over long periods of time. This, too, is clearly true.
And yet, these hand-waving arguments that focus on justifying the creativity of selection do not suffice to address the issue of initiative or dynamics that arises if we attempt to give a dynamically sufficient account of evolution, i.e., if we address evolution explicitly as a process of change. The fundamental problem is that we cannot get the dynamics of evolution right without representing discrete events of the introduction of novelty by mutation-and-altered-development. We must recognize the introduction process as a genuine evolutionary cause.
Once we have added this vital piece of conceptual infrastructure, it then becomes possible to build a larger framework for causal theories. By appealing directly to the introduction process as an alternative type of causation, we can specify complete chains of causation from internal features that determine mutational and developmental propensities of variation, to quantifiable evolutionary behavior, via the population-genetic consequences of biases in the introduction process.
Let us briefly consider how to utilize the concept of biases in the introduction process (as a genuine cause of evolutionary orientation or direction) to specify a causal grounding for 3 historic themes of internalist thinking:
- Taxon-specific propensities
- Intrinsically likely forms
- Directional trends
The first step is to make the transition from mutation biases and nucleotide-level effects to phenotypes. Let varigenesis cover all of the processes involved in the generation of new variation, from mutation to altered phenotypic development, subject to any applicable conditions. In quantitative genetics, varigenesis is represented by the M matrix of variances and covariances for new phenotypic variation (see note 5). For a discrete phenotype-space, we may consider a vector of rates U, with one rate for each alternative phenotype.
In the original Yampolsky-Stoltzfus model, the mutation bias B is a ratio of two mutation rates u1 and u2 , and these are specific mutation rates from one genotype to another.
But when we turn our focus to phenotypes, we can simply redefine u1 and u2 in terms of alternative phenotypes. For instance, consider an example in the figure below, based on the genetic code, which is the genotype-phenotype (GP) map relating codon genotypes to amino acid phenotypes. The rate u1 represents Asp-to-Val and the rate u2 represents Asp-to-Glu, which implicates 2 different mutational paths. Therefore, even if all mutation rates are the same (no mutation bias), the GP map induces a 2-fold phenotypic bias favoring Asp-to-Glu.
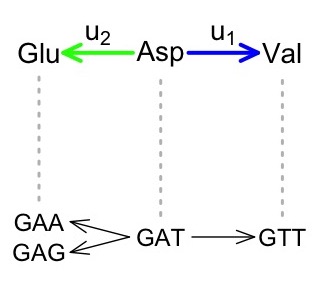

To the extent that fitnesses depend only on the phenotype, the two mutational paths from Asp to Glu are identical and will behave as if this were 1 path with a 2-fold higher rate. In this way, all the same conclusions that apply to a B-fold bias in the Yampolsky-Stoltzfus model will also apply to a B-fold phenotypic bias in varigenesis. That is, a GP map such as the genetic code induces asymmetries in the introduction of alternative phenotypes.
The figure above right represents a precisely analogous idea that is common in the evo-devo literature, which is that some alternative phenotypes may be more likely (in varigenesis) because they implicate a larger number of mutationally accessible genotypes, i.e., genotypic neighbors in the GP map. Here, the 1-mutant neighborhood of a genotype encoding phenotype P0 includes 5 genotypes with phenotype P2, and only 1 with genotype P1. In this case, without any mutation bias per se, there is still a 5-fold phenotypic bias in varigenesis toward P2.
In general, the form of the above argument is to use the neighboring phenotypes implicated by a GP map to define equivalence classes of genotypes, so that we can aggregate mutation rates by equivalence class, with the result that the differential mutational accessibility of alternative phenotypes will emerge due to asymmetries in the GP map, even if all mutation rates are the same. That is, for a given starting genotype, a mutation spectrum at the genotypic level, together with a GP map, induces a description of potentialities or dispositions of phenotypic change in a developmental-genetic system, i.e., a description of varigenesis.
This provides a rigorous justification for the notion that each taxon, having a distinctive genotype and GP map, has an intrinsic evolutionary potential or inherited predisposition, due to propensities of varigenesis.
[Note: reactions at a phil-bio-circle presentation of this piece convince me that the above argument, in order to capture an essential aspect of evo-devo, needs to distinguish arbitrary encodings from other sources of asymmetry in the accessibility of neighboring phenotypes. The example based on the genetic code (above, left) illustrates asymmetries in accessibility that are induced by an abstract and arbitrary digital encoding of biology in the genetics of sequences. That is, the genetic code is a largely arbitrary mapping of triplet genotypes to amino acid phenotypes, and it induces a set of neighbor relationships that are arbitrarily different in degree of mutational connectivity. Why should Asp-to-Val be less connected than Asp-to-Glu? There is no direct biological explanation, e.g., this relationship does not emerge due to Asp and Val sharing biosynthesis pathways. I am well aware of the hypothesis that the genetic code is adaptively organized (see Stoltzfus and Yampolsky, 2009), but this is an indirect effect— calling on an evolutionary process of code changes over vast scales of time— and the effect-size is very small.
This asymmetry due to an arbitrary encoding does not smell right as a rationalization of evo-devo arguments, e.g., in structuralist evo-devo arguments per Newman, the propensities that are attributed to developmental systems reflect the emergent dynamic properties of materials such as cell layers, and not merely the details of an arbitrary encoding.
Nevertheless, the differences in these dynamic properties of materials induced by a change in genotype can be mapped to the discrete space of genotypes, and this mapping will induce asymmetries in accessibility that are subject to the same consequence laws as the asymmetries induced by an arbitrary encoding. Thus the example on the right above, with P1 and P2, is a better match to evo-devo if the relatively higher accessibility of P2 is an effect of development, e.g., the phenocopy effect, and not an effect of arbitrary genetic encoding. From the way the example is given above, we can’t really tell. However, the problem is resolved in the following section, to the extent that the RNA folding example below is precisely the right kind of example: the structure of a GP map, and the propinquity of phenotypes in genotype-space, reflects the self-organizing properties of RNAs, i.e., the folding propensities that arise as emergent properties of each specific RNA sequence. ]
Next, let’s consider the tradition of structuralist arguments to the effect that certain familiar structures or features commonly emerge in nature because they are, in some sense, intrinsically likely, i.e., because they are the most natural or easily generated states of the materials in question.
We already addressed the contemporary form of this argument per Kauffman, which has been made in regard to RNA folds, protein folds, regulatory network structures, and some features of tissue layers: the forms that are intrinsically likely are understood to be the forms that are common in genetic possibility-spaces, and the question of evolutionary causation is what evolutionary cause makes intrinsically likely forms evolutionarily likely.
In regard to RNA folds, the folds with the most sequences occupy the greatest volume in genotype space, thus they have the largest number of mutational arrows pointed at them, including the arrows pointed at them from other regions of genotype space (which is actually a function of surface area rather than volume or cardinality). This means they are more likely to be proposed, thus more likely to be proposed-and-accepted, by an evolutionary process that explores sequence space via mutation.

Thus, it is possible to specify a rigorous causal grounding for the kind of structuralist argument that explains what is evolutionarily likely by referring to what is common in abstract possibility-spaces.
Next, consider the idea of long-term directional trends due to internal biases in variation. Classical thinking says that such trends are impossible, and that (except under the case of neutral evolution) selection is the sole source of direction in evolution. However, models of adaptive walks with protein-coding genes subject to GC or AT biases in mutation show that compositional trends are the predictable result of biases in the introduction process.
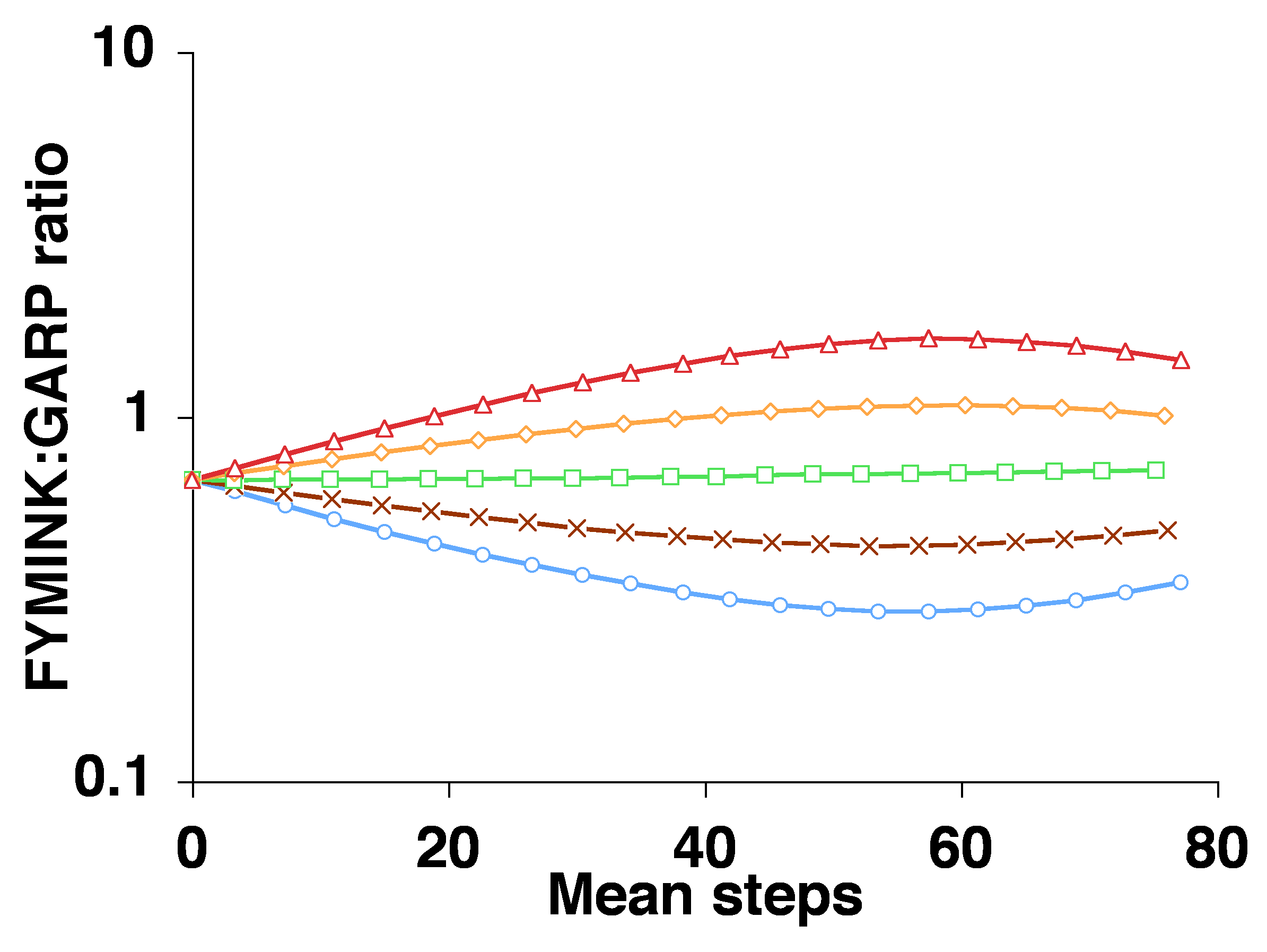
Note that when we collapse evolutionary change down to 1 dimension, the result is that internal and external factors, if they do not coincide in direction, must clash in direction. This way of combining the two types of causes leads to a consideration of which force is stronger, and (given the “pressure” conception of forces) selection is assumed to be the winner of this zero-sum game. But for an evolutionary process operating in a high-dimensional space such as a protein fitness landscape, there are typically many ways to go up, i.e., many directions toward increased fitness, some of them more favored by mutation, and some less favored. As a result, the trajectory of adaptive evolution in a high-dimensional space may have components of direction that are due to fitness effects, and other components of direction that are due to internal variational biases.
Thus, it is possible to specify a rigorous causal grounding for the notion of trends due to internal biases, and we can use this theoretical foundation to rebut the false intuition, widespread in the literature, that strong selection must necessarily suppress the effect of internal tendencies of variation. The source of this intuition is unclear. Does it arise from conceptualizing selection as a governing agent? Is it based on treating evolution as some kind of zero-sum game in which any deviation from a selective ideal is considered a loss? Modeling tells us that, regardless of the source of this intuition, it is mistaken: the same mutation bias will make adaptation easier in some cases and harder in others, depending on circumstances, a point that is illustrated by Cano and Payne (2020) using empirical fitness landscapes.
To summarize, the paragraphs above outline a causal grounding for the classic internalist-structuralist themes of (1) taxon-specific propensities, (2) intrinsically likely forms and (3) directional trends. This is a broad argument but it is not infinitely broad, e.g., it does not propose a new “Synthesis” or try to capture every complaint of every reformer. To suggest this causal grounding does not mean that all past internalist statements are true or even that they are all theoretically possible. Many of these past claims could be stupid. What it means is that, for each of the three classic types of claims identified above, we can map the form of the claim onto a causal model that validates its logic. If we can map a specific internalist claim to a causal model of this form, then it becomes a substantive falsifiable hypothesis about internal causes that can be tested using whatever tools are available to test hypotheses.
“Adaptation has a known mechanism: natural selection acting on the genetics of populations … Thus we have a choice between a concrete factor with a known mechanism and the vagueness of inherent tendencies, vital urges, or cosmic goals, without known mechanism.” (Simpson, 1967, p. 159)
This means that we are in a different place than in 1967 when Simpson wrote the above passage dismissing the notion of internal trends. Simpson’s argument is invalid, and this is not because we have discovered vital urges or cosmic goals, but because we have reconsidered evolutionary genetics both in theory and in fact, and we have concluded that internal biases are a real possibility grounded in the theoretically and empirically demonstrated effects of biases in the introduction process. The influence of such biases is now in the “known mechanism” category, available to be applied in all areas of evolutionary research.
Distinguishing other theories and paradigms
Which theories are (or were) actually used in reasoning about the role of variation in evolution? What roles for variation have been considered explicitly in accounts of evolution? What kinds of reasoning do these theories support, as documented by recurrent and explicit claims in the evolutionary literature? Here are some:
- Variations emerged adaptively by effort, and were preserved, as per Lamarck
- Variation supplied indefinite raw materials that selection shaped into adaptations, as per Darwin.
- The mechanisms of development (and in some versions, the influence of conditions) imposed constraints on variation, setting limits on what is possible, as per Eimer (1898) or Oster and Alberch (1982)
- Mutation pressure drove allele frequencies under neutrality or high mutation rates, per Haldane (1927)
- New quantitative variation (M) contributed to standing variation (G) which, together with selection differentials (β), jointly determined (as Gβ) the short-term rate and direction of multivariate change in quantitative characters (Lande and Arnold, 1983; see note 5).
Relative to these ideas, the theory of the efficacy of biases in the introduction process (as a cause of orientation or direction) is distinctive, i.e., it represents a 6th theory with distinctive and testable implications. The logic of the theory generates various outputs that are otherwise not known to be part of evolutionary reasoning. Indeed, one way to explore this distinctiveness is to use the rhetorical approach of crafting statements that the theory distinctively enables. Such statements can refer, not only to expected evolutionary behavior, but also to other theories, and to informal claims in the literature that may be supported or contradicted, like these:
- Biases in the introduction of variation can impose biases on the course of evolution without requiring neutrality, high mutation rates, or absolute constraints
- Thus, variational biases on the course of adaptation are possible.
- The common assumption in the molecular evolution literature that mutational effects on evolution require or imply neutrality is mistaken
- The Haldane-Fisher argument as expressed by Haldane (1927) or Fisher (1930), and as employed by authors such as Huxley, Ford, Gould, Maynard Smith, et al, does not provide correct reasoning about the potential impact of biases in varigenesis because it fails to cover biases in origination.
- The joint dependence (that emerges under some conditions) of adaptive changes on fixation probability and chance of mutational introduction invites previously unimagined considerations of Berkson’s paradox
- For moderate values of B, there are conditions (e.g., in the origin-fixation regime) under which a B-fold bias in the introduction of variants results in a B-fold bias in evolutionary change
- Biases in mutational accessibility of alternative phenotypes represent a kind of developmental bias, and conditions exist under which this kind of developmental bias may influence evolution in the same way, i.e., by the same kind of population-genetic mechanism, as a mutational bias of the same magnitude
- This result invalidates the historically important argument (by Mayr, Wallace and others) attempting to undermine causal claims of evo-devo on the grounds that development cannot be construed as an evolutionary cause.
- Adaptive traverses of high-dimensional spaces can exhibit, simultaneously, components of direction that reflect fitness effects mediated by selection, and components that reflect biases in varigenesis mediated by the introduction process
- This result invalidates a kind of informal logic (of selection as a governing force) suggesting that internal biases must come at an adaptive cost or that they somehow work against or impede selection
- Systematic biases in the mutational introduction of phenotypic forms (due to their differing surface area in genotype-space) provide a possible population-genetic mechanism for the findability aspect of “self-organization” reported by Kauffman (1993) or the “phenotype bias” reported by Dingle, et al (2021).
The grounding for internalism that emerges from this theory does not map in a simple way to the current reformist literature in evolutionary biology, with its complaints about reductionism, calls for the “return of the organism,” and exploration of the diffuse EES-SET axis of dispute. I don’t see this as a problem: I see it as inevitable. Einstein said that “We can’t solve problems by using the same kind of thinking we used when we created them.” If we accept this logic, then it would be very unlikely for the solution to a long-standing conundrum to map in a neat and clear way to the terms and concepts people have been using all along. The argument here evokes a conflict with a specific aspect of classic thinking, a specific conception of causal forces as mass-action pressures that interferes with productive thinking about the role of generative processes in evolution.
Relative to the classic conception of evolutionary causes as population-level pressures on allele frequencies, the introduction process conflicts with the statistical pressure criterion, but not necessarily the population-level emergence criterion. The introduction process is arguably emergent at the population level: if a specific individual in state A1 mutates to state A2, this is clearly an event of mutation, but we cannot determine whether it is an event of introduction without examining the population of which the individual is a member, i.e., we can’t diagnose an introduction event except at the population level. Again, mutational introduction and mutational conversion are distinct: introduction is emergent at the population level (see note 7).
However, the introduction process is different from classical forces because it is not a deterministic mass-action pressure aggregating over the behavior of countless individual members of a population (see note 3). To characterize the introduction process as a cause is to put the focus on a probability distribution for events that reflect generative processes acting inside organisms. These processes are studied by mutation researchers and developmental biologists.
The main distinction from the “constraints” literature of evo-devo is the concern to specify complete chains of causation from internal features that determine propensities of variation, to quantifiable evolutionary behavior, via population genetics. As explained above, the typical approach in the evo-devo literature, following Maynard Smith, et al (1985), leaves a gap in this chain of causation, where the missing theory would explain how developmental propensities of varigenesis become evolutionary propensities. [Note that Maynard Smith et al did not ignore this issue, but they published a review without filling this gap, and then this review was cited by thousands of other sources.] In the evo-devo literature, efforts to reform thinking about causation typically focus on supplementing population-genetic causation with lineage explanation (Calcott, 2009), rather than rethinking population-genetic causation.
A crucial distinction from the “evolvability” literature and the more recent literature of “developmental bias” in the EES context is that the causal grounding for internalist thinking offered here does not, in any way whatsoever, presume or imply that variation is facilitated, contrary to the fatuous treatment by Svensson and Berger (2019). The literature has been (to my way of thinking) relentlessly confusing on the extent to which the distinctiveness of evo-devo, or the distinctiveness of evolvability claims, is presumed to rest on facilitated variation.
By contrast, the focus here is on consequence laws— consequence laws that apply whether or not any source laws exist that specify facilitated variation. For instance, it is not necessary to assume that the molecular bias for transition over transversion mutations is in some way beneficial (see Stoltzfus and Norris, 2015). The theory predicts an influence of transition bias on adaptation even when the mutation bias is perfectly orthogonal to fitness effects. The issue of whether varigenesis is dispositional in its effect on evolution can be adjudicated entirely separately from whether varigenesis is facilitated or whether organisms are surprisingly evolvable.
Of course, non-orthogonality is inevitable in a high-dimensional world. In the case of any real-world landscape, a mutational bias toward transitions (1) will tend to align the overall process of evolutionary exploration better (quantitatively) with beneficial trajectories, or (2) will tend to align it worse. The modeling study by Cano and Payne (2020) demonstrates this point using empirical fitness landscapes for binding sites.
Perhaps this will seem disappointing for those familiar with the literature of evolvability or the EES Front, where the idea that variation is facilitated, and that living systems are surprisingly “innovable,” is deeply entrenched. Where is the mojo of internalism if internal variational propensities are merely arbitrary and not an expression of the superior evolvability of naturally evolved systems?
Relative to this way of thinking, the proposal here is about learning to walk before trying to run: it emphasizes an issue that is logically prior. Perhaps variation is facilitated, but a dispositional evolutionary role for varigenesis is both the premise and the promise of this claim. It is the zero-order effect that necessarily underlies all possible higher-order effects pertaining to intrinsic variability.
In fact, the notion of taxon-specific propensities of variation that are merely dispositional without being facilitated is historically part of evo-devo, e.g., it was the explicit position of Maynard Smith, et al (1985) that developmental biases are arbitrary. Similarly, the primary argument of Alberch and Gale (1985) is that two different taxa (salamanders and frogs) tend to lose digits differently in evolution (pre- or post-axially) for internal reasons, i.e., they tend to be lost differently when development is perturbed: Alberch and Gale were not arguing that each taxon evolved a better way to lose digits, but merely a different way.
Synopsis
The notion that evolution may have tendencies that reflect internal tendencies of variation is an old idea (see note 4). Yet, evolutionary discourse has proceeded without any rigorous grounding for internalist thinking. In particular, the Haldane-Fisher argument appeared to undermine this kind of theory.
Nevertheless, a rigorous grounding for internalist thinking is possible, based on the theory of biases in the introduction process. The logic of this theory has been validated by mathematical and computer modeling. Empirical studies have shown a strong effect of ordinary mutation biases on the changes involved in adaptation, an effect that is expected under the theory but which is not possible under the mutation pressure theory of Haldane and Fisher.
The kinds of variational tendencies covered by the theory include (1) mutation biases such as transition-transversion bias, (2) local asymmetries induced by the properties of genotype-phenotype (GP) maps, which reflect both arbitrary encoding and the propensities of developmental systems, and (3) differences in findability and connectivity of phenotypic forms induced by broad features of the architecture of genetic spaces.
When this previously missing causal link is considered in the broader context of contemporary internalist arguments, it provides a way to specify complete chains of causation from internal tendencies of variation to quantifiable tendencies of evolution, integrated with the evolutionary genetics of populations, rationalizing key themes of internalist thinking: taxon-specific dispositions, directional trends, and intrinsically likely structures.
This argument is not infinitely broad. It does not purport to cover everything. However, it offers a broad alternative to neo-Darwinism, i.e., we can specify an alternative to neo-Darwinism that can be used to generate hypotheses that provide a causal grounding for common internalist themes— a complete grounding that extends from internal properties to quantifiable evolutionary tendencies, by way of the evolutionary genetics of populations. Because the theory is quantitative, it will be possible, ultimately, to make statements that compare the relative importance of internal factors influencing varigenesis with the importance of selection.
Acknowledgements
I thank Tobias Uller and members of the phil-bio-circle discussion group (particularly Stuart Newman, Alan Love and Sahotra Sarkar) for comments. NIST disclaimer. Charles R. Darwin, who is often credited with ghost-writing contemporary evolutionary work, did not plan, write, review, or contribute in any meaningful way to this manuscript.
References
- Alberch P, Gale EA. 1985. A developmental analysis of an evolutionary trend: digital reduction in amphibians. Evolution 39:8-23.
- Amundson R. 2001. Adaptation, Development, and the Quest for Common Ground. In: Hecht S, Orzack SH, editors. Adaptation and Optimality. New York: Cambridge University Press. p. 303-334.
- Arthur W. 2004. Biased Embryos and Evolution. Cambridge: Cambridge University Press.
- Calcott B. 2009. Lineage Explanations: Explaining How Biological Mechanisms Change. The British Journal for the Philosophy of Science 60:51-78. http://www.jstor.org/stable/25591988
- Eimer T. 1898. On Orthogenesis; and The Impotence of Natural Selection in Species-Formation. Chicago: Open Court Publishing Co.
- Eshel I, Feldman MW. 2001. Optimality and Evolutionary Stability under Short-term and Long-term Selection. In: Orzack SH, Sober E, editors. Adaptationism and Optimality. Cambridge: Cambridge University Press. p. 161-190.
- Fox RF. 1993. Review of Stuart Kauffman, The Origins of Order: Self-Organization and Selection in Evolution. Biophysical Journal 65:2698-2699.
- Gould SJ, Lewontin RC. 1979. The spandrels of San Marco and the Panglossian paradigm: a critique of the adaptationist program. Proc. Royal Soc. London B 205:581-598.
- Hartl DL, Taubes CH. 1998. Towards a theory of evolutionary adaptation. Genetica 103:525-533.
- Lynch M. 2007. The frailty of adaptive hypotheses for the origins of organismal complexity. Proc Natl Acad Sci U S A 104 Suppl 1:8597-8604.
- Maynard Smith J. 1983. Evolution and Development. In: Goodwin BC, Holder N, Wylie CC, editors. Development and Evolution. New York: Cambridge University Press. p. 33-46.
- Mayr E. 1994. Response to John Beatty. Biology and Philosophy 9:357-358.
- McCandlish DM, Stoltzfus A. 2014. Modeling evolution using the probability of fixation: history and implications. Quarterly Review of Biology 89:225-252.
- Michod RE. 1981. Positive Heuristics in Evolutionary Biology. The British Journal for the Philosophy of Science 32:1-36.
- Mitchell, P. Coupling of Phosphorylation to Electron and Hydrogen Transfer by a Chemi-Osmotic type of Mechanism. Nature 191, 144–148 (1961).
- Morgan TH. 1910. The American Society of Naturalists Chance or Purpose in the Origin and Evolution of Adaptation. Science 31:201-210.
- Popov I. 2009. The problem of constraints on variation, from Darwin to the present. Ludus Vitalis 17:201-220.
- Provine WB. 1978. The role of mathematical population geneticists in the evolutionary synthesis of the 1930s and 1940s. Stud Hist Biol. 2:167-192.
- Provine WB. 1971. The Origins of Theoretical Population Genetics. Chicago: University of Chicago Press.
- Shull AF. 1935. Weismann and Haeckel: One Hundred Years. Science 81:443-451.
- Sober E. 1984. The Nature of Selection: Evolutionary Theory in Philosophical Focus. Cambridge, Mass.: MIT Press.
- Stoltzfus A. 2006. Mutation-Biased Adaptation in a Protein NK Model. Mol Biol Evol 23:1852-1862.
- Stoltzfus A. 2017. Why we don’t want another “Synthesis”. Biol Direct 12:23.
- Stoltzfus A. 2019. Understanding bias in the introduction of variation as an evolutionary cause. In: Uller T, Laland KN, editors. Evolutionary Causation: Biological and Philosophical Reflections. Cambridge, MA: MIT Press.
- Tenaillon O. 2014. The Utility of Fisher’s Geometric Model in Evolutionary Genetics. Annu Rev Ecol Evol Syst 45:179-201.
- Ulett MA. 2014. Making the case for orthogenesis: The popularization of definitely directed evolution (1890–1926). Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences 45:124-132.
- Xue JZ, Costopoulos A, Guichard F. 2015. A Trait-based framework for mutation bias as a driver of long-term evolutionary trends. Complexity 21:331-345.
- Yampolsky LY, Stoltzfus A. 2001. Bias in the introduction of variation as an orienting factor in evolution. Evol Dev 3:73-83.
- Yedid G, Bell G. 2002. Macroevolution simulated with autonomously replicating computer programs. Nature 420:810-812.
Notes
1. Classical population genetics does not ignore mutation or treat it solely as a background condition. In particular, classic work pays loads of attention to deleterious mutation pressure. That is, in the case of deleterious mutation pressure, mutation is often treated as a change-making causal process characterized by explicit dynamics. But we are not concerned here with deleterious mutation pressure. We are concerned with the novelty-introducing role of mutation, in situations where this role may lead to changes that are actually incorporated in long-term evolution.
2. We should not be surprised by the lack of generality of the Modern Synthesis, which was never intended to be a general framework, but was constructed deliberately to exclude certain broad classes of ideas. That is, the SGFT and the ideas of causation that emerged mid-century were constructed deliberately to rationalize a neo-Darwinian view and to make alternatives appear unreasonable or impossible, particularly the “mutationist” views of the early geneticists. To some extent, the position developed by Mayr and his cohort of influencers was less like an ordinary scientific theory — driven by the challenge of accounting for empirical patterns — and more like a rhetorical battleship with its guns aimed squarely at alternatives to neo-Darwinism.
In the contemporary literature, the “Synthesis” remains more of a rhetorical strategy than a scientific theory, but now the focus is purely defensive, aimed at developing a flexible rhetorical strategy to fight off calls for reform by shifting the goal-posts, rather than a strategy to vanquish rivals and establish pre-eminence. That is, contemporary defenses of the Synthesis represent a rhetorical posture of defending the fullness and authority of tradition against the claims of reformers, by anchoring all new developments in tradition. The common theme is still the TINA doctrine (There Is No Alternative) yet, whereas this originally meant that one closed and restrictive theory claimed victory and excluded all the others, now it means that one open and flexible tradition appropriates all valuable ideas and claims ownership of them. Unlike the case for an ordinary theory, no risk is allowed in the Synthesis portfolio, i.e., it is alleged to include only well founded claims and positions that are immune to falsification.
By contrast, Provine, in his 2001 re-issue of The Origins of Theoretical Population Genetics, said that the Modern Synthesis “came unraveled” in the 1980s. Because Provine construed the Synthesis orthodoxy mainly as a position on population genetics, he is most concerned with the breakdown of the SGFT and the rise of neutralism. That is, Provine is not associating the demise of the Synthesis with the paleontology challenge (1970s to 1980s) or the evo-devo challenge (1980s onward), but instead with a changing understanding of population genetics primarily due to the challenge from molecular evolution.
3. Note that the conception and use of forces is typically deterministic, e.g., Sober (1984) says that “In evolutionary theory, mutation and selection are treated as deterministic forces of evolution” whereas drift is treated stochastically. Importantly, one may aggregate the effects of the introduction process over infinitely many loci, e.g., all the sites in a genome, and this makes it possible to speak in a technically correct way about a mass-action pressure, but it is a pressure of introduction. Many, many claims in the molecular evolution literature refer to “mutation pressure” (e.g., Lynch 2007) but do not make any sense unless we reinterpret them in terms of introduction pressure. But introduction pressure is a different kind of pressure from the classical forces, operating in a different field: it aggregates over sites or loci in a genome rather than over member organisms in a population. Because it is an entirely different kind of pressure, it has different implications (for more explanation, read this). It would be possible to articulate an alternative theory of forces for evolutionary behavior in a discrete space where the steps are origin-fixation steps (Pablo Razeto-Barry has an unpublished manuscript on this).
4. This old idea is sometimes called “orthogenesis,” but the relentless caricatures by traditional authorities (noted by Ulett, 2009) have given “orthogenesis” such a pejorative connotation that it is not useful to use the term. For a review of historic ideas about constraints or channeling of variation relatively untainted by Darwinian prejudices, see Popov (2009) or Ulett (2014).
5. I’m giving myself a pass to put evolutionary quantitative genetics (EQG) in the background here because foregrounding it would be confusing. The theory is fundamentally phenomenological rather than causal, in the sense that it was not built in a bottom-up way from mechanisms or causes, but specified in a top-down way by the constraint of flexibly capturing the measurable relations of certain important quantities. So, it is always difficult to fathom EQG in a discussion of causes, though clearly the original motivation was tied to a neo-Darwinian view of variation as raw materials, i.e., variation (passive object) as a material cause, not varigenesis (active process) as an agent with dispositional effects. Because raw materials are just raw materials, providing substance only and not form, the only meaningful question to ask about them is some version of “how much do I have?” But if variation is seen as a dynamic process operating in a multidimensional space, then we have lots of questions to ask, or (stated differently) lots of ways to parameterize it.
Apropos, EQG following on the multivariate generalization of Lande and Arnold (1983) is no longer strictly aligned with neo-Darwinism, but became a formalism with the (initially cryptic) potential to support more causally oriented theorizing with varigenesis as a dispositional factor in evolution via M, although quantitative geneticists themselves have no love for this idea, and it has only a limited scope because the entire framework has a limited scope. The framework, by original conception, only applies to quantitative traits with abundant infinitesimal variation, and the typical implementations treat dimensional heterogeneity but not directional bias. That is, varigenesis (M) represents a process that generates different amounts of abundant infinitesimal raw material in different multivariate dimensions. It can generate more variation along some dimension, but biases in one direction (along a dimension) are usually not considered, and when they are considered, they are not found to be important (except Xue, et al 2015 find support for directional trends in a quantitative character, albeit with a non-standard approach).
The ultimate point here is that EQG also provides a specific and rigorous theoretical grounding for internalist thinking, one that is taken very seriously by some leading thinkers (e.g., Thomas Hansen and Günter Wagner), but this grounding is of such limited utility that I’m finding it convenient to set aside for my purposes here, e.g., it doesn’t provide a way to rebut the Haldane-Fisher argument, to account for directional trends or mutation-biased adaptation, or to justify findability claims. However, I am open to being convinced, by someone who knows better, that EQG provides a broader causal grounding for internalism than I have suggested.
6. A folk theory of biases in the introduction process emerged in an odd place: the macroevolution debate of the 1970s and 1980s. The participants in this debate quickly reached a consensus that no new fundamental mechanisms were needed to account for macroevolution, only a hierarchical expansion of existing mechanisms, i.e., an expansion from the traditional level of a population of individuals, to all the levels in a hierarchy of populations (cells, individuals, species, higher taxa).
However, in the process of this expansion, some of the participants creatively misinterpreted traditional thinking. In particular, Vrba and Eldredge (1984) depicted evolution as a dual process of the introduction and reproductive sorting (by selection and drift) of variants, and they emphasized that evolutionary biases could emerge from either introduction or sorting. Based on this formula, they helpfully reinterpreted evo-devo statements (Rachootin and Thompson; Oster and Alberch) to mean that “bias in the introduction of phenotypic variation may be more important to directional phenotypic evolution than sorting by selection.” That is, their elegantly stated verbal theory (1) recognizes, as distinct phases of the evolutionary process, the production or introduction of variation, and the reproductive sorting of variation (by selection and drift), (2) in parallel, distinguishes biases in introduction from biases in sorting as alternative causes of evolutionary bias, and (3) generalizes this theory of dual causation to multiple levels of a hierarchy.
In this way, Vrba and Eldredge (1984) proposed a novel quasi-mutationist theory of evolution as a process of mutation proposes, sorting disposes. However, the theory lacked any model or formalization, so it was not possible to generate quantitative expectations or offer any proofs. Furthermore, participants in the macroevolution debate did not treat this as a radical proposal demanding validation, because it was presented (mistakenly) as merely a restatement of orthodoxy. That is, whereas Maynard Smith et al (1985) recognized the conflict between implicit evo-devo theories and classical population genetics— presumably because the authors included Maynard Smith, Lande and Kauffman (individuals with expertise in formal theory)—, Vrba and Eldredge did not. Their language continues to reverberate in the paleontology literature, but the issues of causation have never been clarified, to my knowledge.
(7) Here and elsewhere I refer to the introduction process in a general way, because it is a generally useful idea that goes beyond mutational origination. Various processes that we do not normally consider as mutation can introduce discrete genetic novelties, e.g., events of lateral transfer, inter-compartmental transfer, recombination, and endosymbiogenesis. Further, large classes of evolutionary processes feature dynamic dependence on events of introduction. In island biogeography, for instance, we can conceptualize a dual process of introduction (a gravid fly is blown to an island) and establishment (an immigrant fly gives rise to a persistent lineage on the island), such that biases in either stage would be effectual. Adaptive dynamics could be seen as a dual proposal-acceptance (introduction-invasion) process, subject to biases in introduction. Cases of cultural evolution such as the evolution of ideas or of language likewise could be treated with origin-fixation dynamics. Per Vrba and Eldredge (1984), the birth of a species is an event of introduction in a hierarchy of levels. I suspect that the origin-fixation formalism typically is not applied in these fields, although I have seen a case of its application to neologisms in language evolution.
In a discrete world, there is always an event that introduces something novel, i.e., an event that makes the step from a frequency of 0 to a frequency of 1/N. However, in the world of modeling, or perhaps in the physical world, there may be cases in which it is useful to define the introduction process as the transient of a continuous value as it departs from 0. Certainly one may foresee, for the case of evolutionary dynamics, conditions under which the dynamics of this departure from 0 are dominated by the contribution of mutation from other alleles even when other processes are operating simultaneously (indeed, there was such a deterministic treatment in Yampolsky and Stoltzfus, 2001).
8. Traditionalists will certainly respond to this kind of claim by quote-mining the canon to find scraps that show Fisher and Haldane paying attention to some aspect of mutation or mutation rates, and objecting on this basis that of course Fisher and Haldane recognized the importance of new mutations or the rates of occurrence of beneficial mutations. However, our focus here is on scientific theories— not on people or vague suggestions—, and particularly on the theories that have shaped evolutionary discourse by being written down, formalized, shared, taught, and applied, i.e., theories and theory-based arguments that actually matter because they drive research, they are used in explanations, and they are used in arguments, e.g., certain Synthesis positions on causation (levels, types, forces) were used in the 1980s and 1990s to make evo-devo reformists sit down and shut up, i.e., these ideas of causation performed real work in evolutionary discourse, making them important. If Haldane secretly recanted his mutation pressure argument from 1927, 1932, and 1933, or if he offered an alternative mutationist theory in a later piece that had no influence, this is irrelevant both to science and (as a first approximation) to scientific history. Perhaps Haldane was secretly a mutationist. Perhaps he also was secretly a Christian and a capitalist. Who cares? Meanwhile, the Haldane-Fisher argument is a genuine argument used repeatedly in evolutionary discourse. It is not in any sense a straw-man argument: it is an argument that matters in a way that can be documented. So long as the canon defining the historical discourse on evolution includes sources like Fisher (1930), Huxley (1942) or Haldane (1932), the Haldane-Fisher argument is part of evolutionary thought, a documented and readily recognizable thread woven into the 20th century discourse on evolution.
A great deal of damage has been done in recent evolutionary discourse by the conflation of arguments about the novel scientific significance of an idea and the primarily cultural arguments that attempt to anchor the idea in tradition. A measure of the genuine scientific novelty of idea X in disciplinary matrix Y is the extent to which practitioners in Y would benefit from integrating X, or the extent to which they are currently reasoning incorrectly due to a lack of awareness of X. This has almost nothing to do with the ability to anchor X in the relevant historical canon, particularly if those who are practicing the art of back-projection have very low standards and are subject to confirmation bias, as is the case in evolutionary discourse. For instance, a press release regarding the demonstration of mutation-biased adaptation by Cano, et al 2022 makes this about “helping to return Darwin’s second scenario [of evolution by new mutations] to its rightful place in evolutionary theory.”
9. Apropos of note 8, the process of historical distortion through back-projection — the projection of contemporary views backwards onto intellectual progenitors — is evident in regard to Fisher’s geometric model, e.g., in Tenaillon (2014). The supplement to Stoltzfus (2017) explains this transmogrification, and Rockman (2012) makes essentially the same point in a footnote. Fisher’s original argument suited a deterministic world in which an allele is chosen by selection if it is beneficial, regardless of the degree of beneficiality, so that the problem of the size distribution of changes in evolution is solved completely by solving for the chance of beneficiality as a function of effect-size. A fully explicit version of Fisher’s argument would go like this:
- the population has a set X of alleles with some distribution of effect-sizes, whose presence is logically prior to selection, so that it implicitly reflects a generative process (in Fisher’s version, this is implicitly a random sample of mutation vectors in the geometric space),
- within X there is a subset X’ with s > 0,
- selection will choose every member of X’ deterministically,
- finally, the geometric model gives the chance that an allele is beneficial, i.e., is a member of X’, as a function of effect-size,
That is, the geometric model yields the chance that an allele is a member of the set that is chosen deterministically by selection. Kimura took the explicit part of this argument, the geometric model, and embedded it within a stochastic origin-fixation conception of evolution, so that effect-size of the benefit becomes important. That is, Kimura took proposition (3) and replaced it with “selection will choose from X’ in proportion to the chance of fixation” (e.g., 2s). Not only is this mutationist innovation contrary to Fisher’s thinking, it utterly changes the conclusion of the argument to favor intermediate-sized changes instead of infinitesimal ones. Yet, contemporary authors use “Fisher’s model” to describe Kimura’s model, and imply that Fisher shared Kimura’s mutationist conception of evolution but made a mistake or was confused about how to calculate the result. Again, see Stoltzfus (2017) or Rockman (2012).
10. Wright, in addition to invoking a continuous space of allele frequencies, also depicted a discrete space, a connected network of genotypic nodes. He claimed that the two representations were equivalent, which shows that he did not think this through very carefully. If we imagine a network of the 8 genotypes that form from combinations of alleles at 3 loci (each with 2 alleles), and we imagine the focal system being placed on one of these nodes in the network, we will get a completely different set of expectations about how evolution works than if we imagine the focal system as a point in the 3-dimensional space of allele frequencies. To make evolution in the discrete space act even remotely like evolution in the continuous one, we must instead distribute the probability density of the focal system over the entire discrete network.