Updates to Mutation, Randomness and Evolution

November 3, 2023 / Arlin Stoltzfus / 0 Comments

Table of Contents

Most recent update: 3 November, 2023, initial version. See the change-log at the bottom for details.

This is an ongoing list of updates and corrections to Mutation, Randomness and Evolution, including typographic errors, as well as substantive errors and updates to knowledge.

Typos and glitches

The following mistakes (given in order, by section number) might be confusing or misleading:

  • section 1.1 refers 3 times to a “50-fold range” of mutation rates in MacLean, et al (2010), but the actual range is 30-fold.
  • section 2.3. See the note about 1.1 (30-fold, not 50-fold)
  • in section 4.3, replace “development, growth, and hereditary” with “development, growth, and heredity”
  • section 4.5 describes a hypothetical experiment examining 20 mutations each for 5 species, then refers to “our small set of 20 X 10” mutations instead of “our small set of 20 X 5” mutations
  • section 5.7, the reference to the “ongoing commitment of evolutionary biologists to neo-Darwinism” is actually refering to the second aspect of neo-Darwinism, i.e., not adaptationism but the dichotomy of roles in which variation is subservient to selection
  • Fig 9.7 right panel title refers to “Frequency rate vs. fitness” instead of “Mutation rate vs. fitness”
  • section 9.3. See the note about 1.1 (30-fold, not 50-fold)
  • section A.3, the equation is mis-formatted. The left-hand side should be xi+1, not xi + 1

More recent work on topics covered in MRE

MRE was mostly completed in 2019 and only has a few citations to work published in 2020. For perspectives more up-to-date, see the following.

Specific updates and clarifications

Ch. 8 covers the theory of arrival bias, and Ch. 9 covers evidence. Both chapters suggest generalizations that are subject to further evaluation. Most of the updates are going to involve these two chapters.

Prediction regarding self-organization (MRE 8.11)

For a long time, I’ve been arguing that one sense of “self-organization” in the work of Kauffman (1993) and others is an effect of findability that is related to the explanation for King’s codon argument, arising from biases in the introduction process (Stoltzfus, 2006, 2012). MRE 8.11 calls this “the obvious explanation for the apparent magic of Kauffman’s ‘self-organization'”, and suggests how to demonstrate this directly by implementing an artificial mutation operator that samples equally by phenotype.

This demonstration has been done— independently of my suggestions— by Dingle, et al. (2022), Phenotype Bias Determines How Natural RNA Structures Occupy the Morphospace of All Possible Shapes. The findability of intrinsically likely forms has been explored in an important series of studies from Ard Louis’s group. The earliest one, Schaper and Louis (2014), actually appeared before MRE was finished (I saw it but did not grasp the importance). More recent papers such as Dingle, et al. (2022) have made it clear that the “arrival of the frequent” or “arrival bias” in this work is a reference to biases in the introduction process that favor forms (phenotypes, folds) that are over-represented (i.e., frequent) in genotypic state-space.

A variety of think-pieces have speculated about what is the relationship of self-organization to natural selection (Johnson and Lam, 2010; Hoelzer, et al, 2006; Weber and Depew, 1996; Glancy, et al 2016; Demetrius, 2023; Batten, et al 2008). In my opinion, all of this work needs to be updated to take into account what Louis, et al. have demonstrated.

Prediction regarding Berkson’s paradox (MRE 8.13)

Berkson’s paradox refers to associations induced by conditioning, often illustrated by an example in which a negative correlation is induced in a selected sub-population, e.g., the wikipedia page explains how a negative correlation between looks and talent could arise among celebrities if achieving celebrity status is based on a threshold of looks + talent. MRE 8.13 suggests that something like this will happen in nature, because the changes that come to our attention in spite of the disadvantage of a lower mutation rate will tend to have a larger fitness advantage, and vice versa.

Data on clonal hematopoesis lines from Watson and Blundell (2022) showing a negative correlation between growth advantage (left) and inferred mutation rate (right)

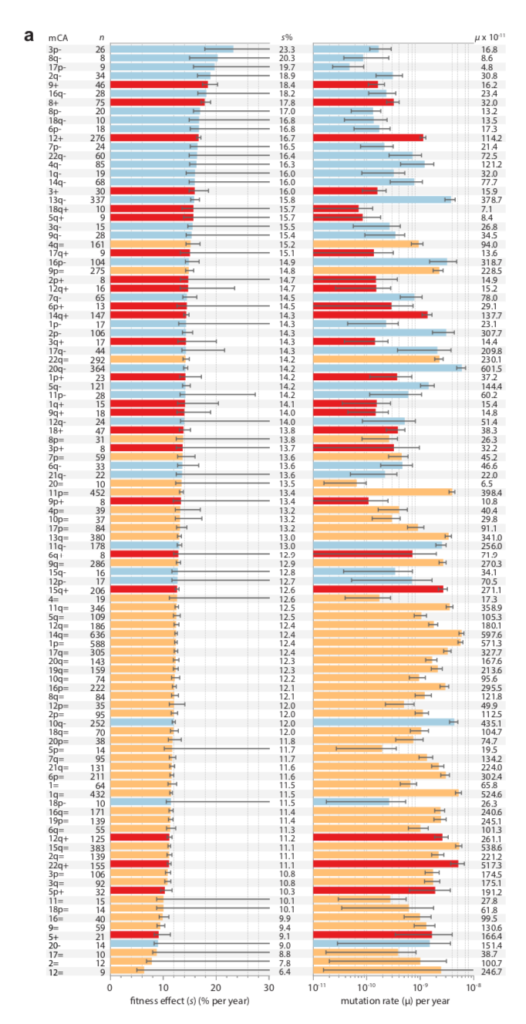
There is now a theory for this, and suggestive evidence (e.g., figure above). In “Mutation and selection induce correlations between selection coefficients and mutation rates,” Gitschlag, et al (2023) address the transformation of a joint distribution of mutation rates and selection coefficients from (1) a nominal distribution of starting possibilities, to (2) a de novo distribution of mutations (the nominal sampled by mutation rate), to (3) a fixed distribution (the de novo sampled by fitness benefit). The dual effect of mutation and selection can induce correlations, but they are not necessarily negative: they can assume any combination of signs. Yet, Gitschlag, et al (2023) argue that natural distributions will tend to have the kinds of shapes that induce negative correlations in the fixed distribution. They use simulations to illustrate these points with realistic data sets. They also show a relatively clear example in which, for the fixed distribution, selection coefficients (estimated from deep mutational scanning) are amplified for a rare mutational type, namely double-nucleotide mutations among TP53 cancer drivers. That is, the drivers that rise to clinical attention in spite of having much lower mutation rates, have greater fitness benefits that (post hoc, via conditioning) offset these lower rates.

MRE 8.13 frames this as an issue of conditioning, but that is only if one is looking backwards, making inferences from the fixed distribution. The forward problem of going from the nominal to the de novo to the fixed can be treated as an issue of what is called “size-biasing” in statistics.

Apropos of this, I realized too late that the problem of conditioning undermines an argument from Stoltzfus and Norris (2015) that is repeated in the book (Box 9.1 or section 9.8.1). When investigating the conservative transitions hypothesis, Stoltzfus and Norris (2015) found that transitions and transversions in mutation-scanning experiments have roughly the same DFE. They also considered the DBFE (distribution of beneficial fitness effects) from laboratory adaptation experiments, which showed that beneficial transversions are slightly (not significantly) better than beneficial transitions.

At the time, this was humorously ironic: not only did we fail to find support for 50 years of lore, the data on adaptive changes actually gave the advantage to transversions.

However, we were attempting to make an inference about the nominal distribution from the fixed distribution, and therefore our inference was subject to conditioning in a way that made it unsafe: transversions that appear in the fixed distribution, in spite of their lower mutation rates, might have greater fitness benefits that (via conditioning) offset these lower rates. Thus, the pattern of more strongly beneficial transversions in the fixed distribution suggests (weakly, not significantly) a Berkson-like effect, but it does not speak against the hypothesis that the nominal DBFE is enriched for transitions (a hypothesis that, to be clear, has no direct empirical support).

Prediction about graduated effects (MRE 9.8.2)

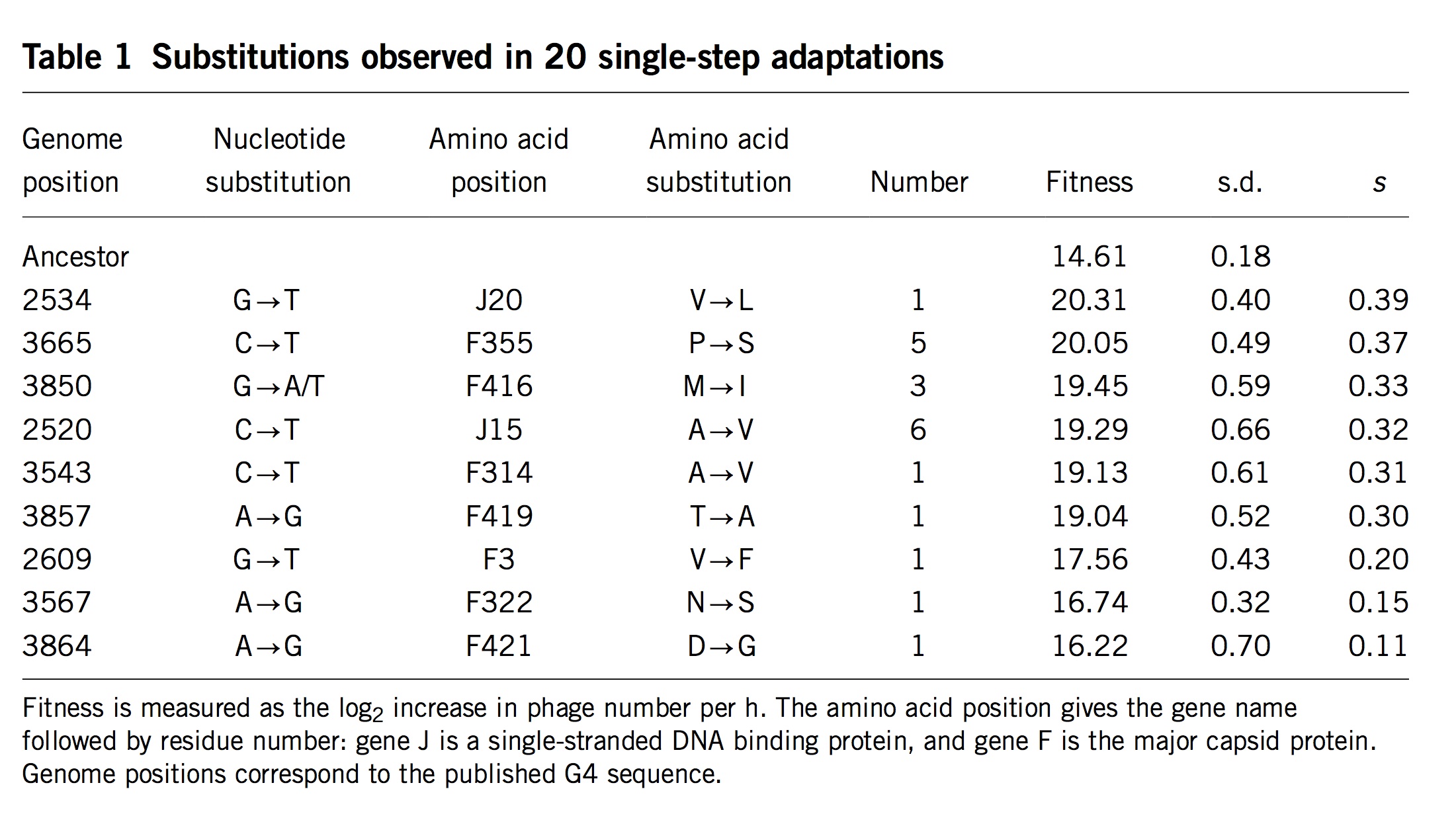
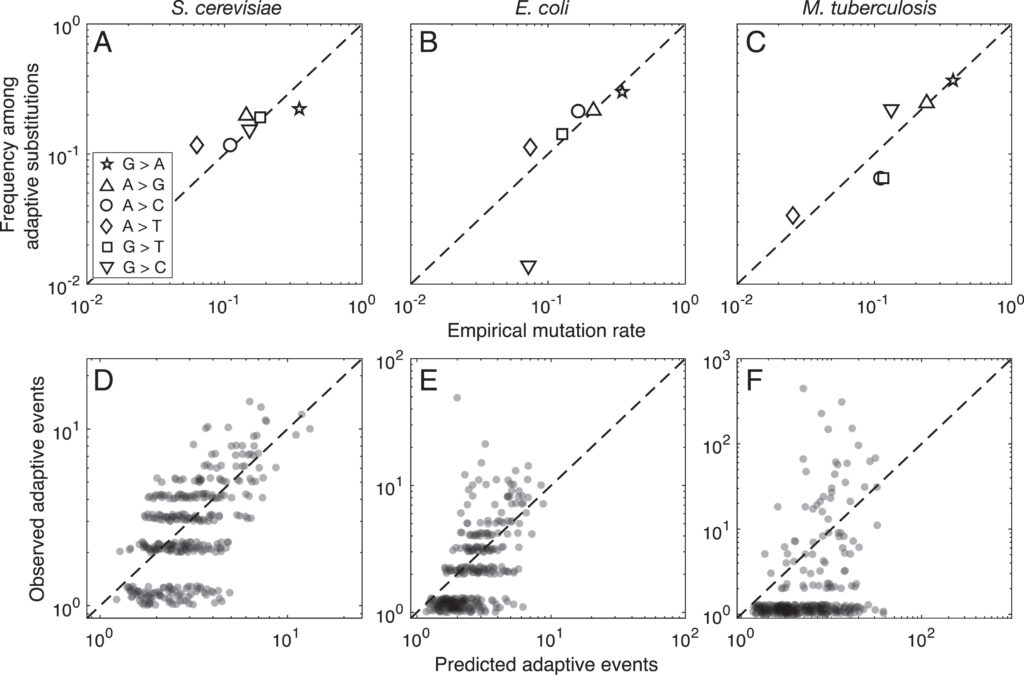
As of 2020, all of the statistical evidence for mutation-biased adaptation in nature was based on testing for a simple excess of a mutationally favored type of change, relative to a null expectation of no bias. As MRE 9.8.2 explains, this is perfectly good evidence for mutation-biased adaptation, but not very specific as evidence for the theory of arrival biases. The theory predicts graduated effects, such that (other things being equal) a greater bias has a greater effect. In the weak-mutation regime, the effects are not just graduated, but proportional.

Evidence for this kind of graduated effect is now available in “Mutation bias shapes the spectrum of adaptive substitutions” by Cano, et al. (2022). The authors show a clear proportionality between the frequencies of various missense changes among adaptive substitutions, and the underlying nucleotide mutation spectrum (measured independently). They also developed a method to titrate the effect of mutation bias via a single coefficient β, defined as a coefficient of binomial regression for log(counts) vs. log(expected). Thus, one expects β to range from 0 (no effect) to 1 (proportional effect). Cano, et al. (2022) found that β is close to 1 (and significantly greater than 0) in three large data sets of adaptive changes from E. coli, yeast, and M. tuberculosis. They also split the mutation spectrum into transition bias and other effects, and found that β ~ 1 for both parts.

What this suggests generally is that each species will exhibit a spectrum of adaptive changes that reflects its distinctive mutation spectrum in a detailed quantitative way. This is precisely what the theory of arrival bias predicts, in contrast to Modern Synthesis claims (about the irrelevance of mutation rates) documented in MRE 6.4.3.

Note that the theory of arrival bias predicts graduated effects under a broad range of conditions, but only predicts β ~ 1 when the mutation supply μN is sufficiently small. Cano, et al. (2022) present simulation results showing how, as μN increases, the expected value of β drops from 1 to 0. This result applies to finite landscapes: for infinite landscapes, the effect of mutation bias does not disappear at high mutation supply (see Gomez, et al 2020).

Misleading claim: “this is expected..” (MRE 8.13)

The section on conditioning and Berkson’s paradox (see above) has the following interpretation of a result from Stoltzfus and McCandlish (2017):

When we restrict our attention to events with greater numbers of occurrences, we are biasing the sample toward higher values of μs. Thus, we expect higher values of μ, higher values of s, and a stronger negative correlation between the two. In fact, Table 9.4 shows that the transition bias tends to increase as the minimum number of occurrences is increased. This is expected, but it does not mean that the fitness effects are any less: again, we expect both higher μ and higher s, as the number of recurrences increases

The dubious part is “This is expected.” There may be a reason to expect this (I’m not entirely sure), but upon reflection, it does not relate to the paradox of conditioning that is the topic of this section, therefore the statement is misleading in context. The part that says “Thus, we expect” follows from conditioning. But the next “This is expected…” claim, if it is indeed correct, would relate to the compounding of trials. For parallelism, i.e., paths with 2 events, the effect of a bias on paths is linear and the effect of a bias on events is squared (see MRE 8.12). If we are considering only paths with 3 events or more, then we can expect an even stronger effect of mutation bias on the bias in events, because counting outcomes by events (rather than paths) is like raising the effect-size of the bias to a higher power. That is, conditioning on 3, 4 or more events per path will enrich for mutations with higher rates, whether they are transitions or transversions, but (so far as I understand) will not enrich for transition bias in the underlying paths.

Poorly phrased: “the question apparently was not asked, much less answered” (MRE 8.14)

This statement— in regard to whether 20th-century population genetics addressed the impact of a bias in introduction— sounds broader than it really is. Clearly Haldane and Fisher asked, and answered, a question about whether biases in variation could influence the course of evolution. The problem is that they didn’t ask the right question, which is about introduction biases. I’m not aware of any 20th-century work of population genetics that asks the right question. The closest is Mani and Clark, which treats the order of introductions as a stochastic variable that reduces predictability and increases variance (whereas if they had treated a bias they would have discovered that it increases predictability).

So, the claim is correct, but it is less meaningful than it sounds. Clearly the pioneers of evo-devo raised the issue of a causal link between developmental tendencies of variation and tendencies of evolution. In response, Maynard Smith, et al (1985) clearly and explicitly raised the question of how developmental biases might “cause” evolutionary trends or patterns. As recounted in MRE 8.8 and 10.2, they did not have a good answer. In general, historical evolutionary discourse includes both pre-Synthesis thinking (orthogenesis; mutational parallelisms per Vavilov or Morgan) and post-Synthesis thinking (evo-devo; molecular evolution) in which tendencies of variation are assumed or alleged to be influential, but the problem of developing a population-genetic theory for this effect was not apparently solved in the 20th century (a substantial failure of population genetics to serve the needs of evolutionary theorizing).

General issues needing clarification

Stuff that isn’t quite right, but which does not have an atomic fix.

Causal independence and statistical non-correlation

In the treatment of randomness in MRE, causal independence and statistical non-correlation are often treated as if they are the same thing. I confess that sorting this out and keeping it straight, without unduly burdening the reader, was beyond my capabilities.

The phrase “arrival bias”

The phrase “arrival of the fittest” or “arrival of the fitter” is used only twice in MRE, to refer to the thinking of others. I missed an opportunity to capitalize on “arrival bias”, a very useful and intuitive way to refer to biases in the introduction process, e.g., as in Dingle, et al (2022). Referring to the “arrival of the fittest” sounds very clever, but it combines effects of introduction and fitness in a way that is unwelcome for my purposes. Strictly speaking, arrival bias in the sense of introduction bias is an effect of the arrival of the likelier (i.e., mutationally likelier), not arrival of the fitter. One version is the “arrival of the frequent” concept of Schaper and Louis (2014), meaning a tendency for mutation to stumble upon the alternative forms that are widely distributed in genotype space.

Note that, by contrast, when Wagner (2015) refers to “the arrival of the fittest”, this is not an error of confounding mutation and fitness, but a deliberate attempt to tackle the problem of understanding how adaptive forms originate.

Quantitative evolutionary genetics

In the past, I mostly ignored QEG as irrelevant to my interests in the discrete world of molecular evolution. But in preparing to write MRE, I invested serious effort in reading the QEG literature and integrating it into my thinking about variation and causation. The biggest gap is the lack of an explanation of how and why the dispositional role of variation differs so radically in the QEG framework as compared to the kinds of models we use to illustrate arrival bias. This gap exists because the problem is unsolved.

Another issue that does not come out clearly is what, precisely, is the position of skepticism in Houle, et al. (2017), and more generally, what is the nature and extent of the neo-Darwinian refugium (or perhaps, redoubt) in the field of quantitative genetics? I incorrectly stated in MRE 5.7 that Houle, et al (2017) favor a correlational-selection-shapes-M theory, whereas their explicit position is that no known model fits their data (this position is better reflected in MRE 9.7). I am struck by the fact that the data on M:R correlation from quantitative genetics is far more rigorous and convincing than various indirect arguments of the same general form in the evo-devo literature, and yet, while the importance of “developmental bias” is often depicted as an established result in the literature of evo-devo (and EES advocacy), quantitative geneticists are clearly hesitant to conclude that the M:R correlation reflects M –> R causation, e.g., see the reference to “controversial” in the first sentence of the abstract of Houle, et al., or in Rohner and Berger (2023).

This is related to the first problem above. Variational asymmetries do not have a lot of power in the standard QEG framework: they are easily overwhelmed by selection. The quantitative geneticists understand this (and the evo-devoists perhaps do not). However, available QEG theory on effects of directional (as opposed to dimensional) bias is limited only to showing how a bias causes a slight deflection from the population optimum on a 1-peak landscape (Waxman and Peck, 2003; Zhang and Hill, 2008; Charlesworth, 2013), and lacks the kinds of multi-peak or latent-trait models that IMHO are going to show stronger effects (Xue, et al. 2015). It will be interesting to see how this plays out.

Change log

3 November 2023. Initial version with typos, updates (with a couple of figures) and Table of Contents.

Understanding the Mutational Landscape Model

October 2, 2015 / Arlin Stoltzfus / 0 Comments

This post started out as a wonky rant about why a particular high-profile study of laboratory adaptation was mis-framed as though it were a validation of the mutational landscape model of Orr and Gillespie (see Orr, 2003), when in fact the specific innovations of that theory were either rejected, or not tested critically.  As I continued ranting, I realized that there was quite a bit to say that is educational, and I contemplated that the reason for the original mis-framing is that this is an unfamiliar area, such that even the experts are confused— which means that there is a value to explaining things.

The crux of the matter is that the Gillespie-Orr “mutational landscape” model has some innovations, but also draws on other concepts and older work.  We’ll start with these older foundations.

Origin-fixation dynamics in sequence space

First, the mutational landscape model draws on origin-fixation dynamics, proposed in 1969 by Kimura and Maruyama, and by King and Jukes (see McCandlish and Stoltzfus for an exhaustive review, or my blog on The surprising case of origin-fixation models).

In origin-fixation models, evolution is seen as a simple 2-step process of the introduction of a new allele, and its subsequent fixation (image).  2_step_cartoonThe rate of change is then characterized as a product of 2 factors, the rate of mutational origin (introduction) of new alleles of a particular type, and the probability that a new allele of that type will reach fixation.  Under some general assumptions, this product is equal to the rate of an origin-fixation process when it reaches steady state.

Probably the most famous origin-fixation model is K = 4Nus, which uses 2s (Haldane, 1927) for the probability of fixation of a beneficial allele, and 2Nu (diploids) for the rate of mutational origin.  Thus K = 4Nus is the expected rate of changes when we are considering types of beneficial alleles that arise by mutation at rate u, and have a selective advantage s.  But we can adapt origin-fixation dynamics to other cases, including neutral and deleterious changes. If we were applying origin-fixation dynamics to meiotic bursts, or to phage bursts, in which the same mutational event gives rise immediately to multiple copies (prior to selection), we would use a probability of fixation that takes this multiplicity into account.

In passing, note that origin-fixation models appeared in 1969, and we haven’t always viewed evolution this way.  The architects of the Modern Synthesis rejected this view— and if you don’t believe that, read The Shift to Mutationism is Documented in Our Language or The Buffet and the Sushi Conveyor.   They saw evolution as more of an ongoing process of “shifting gene frequencies” in a super-abundant “gene pool” (image).  1_step_cartoon Mutation merely supplies variation to the “gene pool”, which is kept full of variation.  The contribution of mutation is trivial.   The available variation is constantly mixed up by recombination, represented by the egg-beaters in the figure.  When the environment changes, selection results in a new distribution of allele frequencies, and that’s “evolution”— shifting gene frequencies to a new optimum in response to a change in conditions.

This is probably too geeky to mention, but from a theoretical perspective, an origin-fixation model might mean 2 different things.  It might be an aggregate rate of change across many sites, or the rate applied to a sequence of changes at a single locus.  The mathematical derivation, the underlying assumptions, and the legitimate uses are different under these two conditions, as pointed out by McCandlish and Stoltzfus.  The early models of King, et al were aggregate-rate models, while  Gillespie, (1983) was the first to derive a sequential-fixations model.

Second, the mutational landscape model draws on Maynard Smith’s (1970) concept of evolution as discrete stepwise movement in a discrete “sequence space”.  More specifically, it draws on the rarely articulated locality assumption by which we say that a step is limited to mutational “neighbors” of a sequence that differ by one simple mutation, rather than the entire universe of sequences.  The justification for this assumption is that double-mutants, for instance, will arise in proportion to the square of the mutation rate, which is a very small number, so that we can ignore them.  Instead, we can think of the evolutionary process as accessing only a local part of the universe of sequences, which shifts with each step it takes. In order for adaptive evolution to happen, there must be fitter genotypes in the neighborhood.

This is an important concept, and we ought to have a name for it.  I call it the “evolutionary horizon”, because we can’t see beyond the horizon, and the horizon changes as we move.  horizonNote two things about this idea.  The first is that this is a modeling assumption, not a feature of reality.  Mutations that change 2 sites at once actually occur, and presumably they sometimes contribute to evolution.  The second thing to note is that we could choose to define the horizon however we want, e.g., we could include single and double changes, but not triple ones.   In practice, the mutational neighbors of a sequence are always defined as the sequences that differ by just 1 residue.

Putting these 2 pieces together, we can formulate a model of stepwise evolution with predictable dynamics.

mut_landscape_numberline Making this into a simulation of evolution is easy using the kind of number line shown at left. Each segment represents a possible mutation-fixation event from the starting sequence.  For instance, we can change the “A” nucleotide that begins the sequence to “T”, “C” or “G”.  The length of each segment is proportional to the origin-fixation probability for that change (where the probability is computed from the instantaneous rate).  To pick the next step in evolution, we simply pick a random point on the number line. Then, we have to update the horizon— recompute the numberline with the new set of 1-mutant neighbors.

Where do we get the actual values for mutation and fixation?  One way to do it is by drawing from some random distribution.  I did this in a 2006 simulation study. I wasn’t doing anything special.  It seemed very obvious at the time.

rokyta_fitnesses

(Table 1 from Rokyta, et al)

Surprisingly, researchers almost never measure actual mutation and selection values for relevant mutants.  One exception is the important study by Rokyta, et al (2005), who repeatedly carried out 1-step adaptation using bacteriophage phiX174.  The selection coefficients for each of the 11 beneficial changes observed in replicate experiments are shown in the rightmost column, with the mutants ranked from highest to lowest selection coefficient.  Notice that the genotype that recurred most often (see the “Number” column) was not the alternative genotype with the highest fitness, but the 4th-most-fit alternative, which happened to be favored by a considerable bias in mutation. Rokyta, et al didn’t actually measure specific rates for each mutation, but simply estimated average rates for different classes of nucleotide mutation based on an evolutionary model.

Then Rokyta, et al. developed a model of origin-fixation dynamics using the estimated mutation rates, the measured selection coefficients, and a term for the probability of fixation customized to account for the way that phages grow. This model fit the data very well, as I’ll show in a figure below (panel C in the final figure).

The mutational landscape model

Given all of that, you might ask, what does the mutational landscape model do?

This is where the specific innovations of Orr and Gillespie come in.  Just putting together origin-fixation dynamics and an evolutionary horizon doesn’t get us very far, because we can’t actually predict anything without filling in something concrete about the parameters, and that is a huge unknown.  What if we don’t have that?  Furthermore, although Rokyta, et al implicitly assumed a horizon in the sense that they ignored mutations too rare to appear in their study, they never tackled the question of how the horizon shifts with each step, because they only took one step.  What if we want to do an extended adaptive walk?  How will we know what is the distribution of fitnesses for the new set of neighbors, and how it relates to the previous distribution?  In the simulation model that I mentioned previously, I used an abstract “NK” model of the fitness of a protein sequence that allowed me to specify the fitness of every possible sequence with a relatively small number of randomly assigned parameter values.

Gillespie and Orr were aiming to do something more clever than that.  Theoreticians want to find ways to show something interesting just from applying basic principles, without having to use case-specific values for empirical parameters.  After all, if we insert the numbers from one particular experimental system, then we are making a model just for that system.

rokyta_fig1

(Figure 1 of Rokyta, et al, explaining EVT)

The first innovation of Orr and Gillespie is to apply extreme value theory (EVT) in a way that offers predictions even if we haven’t measured the s values or assumed a specific model.  If we assume that the current genotype is already highly adapted, this is tantamount to assuming it is in the tail end of a fitness distribution.  EVT applies to the tail ends of distributions, even if we don’t know the specific shape of the distribution, which is very useful.  Specifically, EVT tells us something about the relative sizes of s as we go from one rank to the next among the top-ranked genotypes: the distribution of fitness intervals is exponential.  This leads to very specific predictions about the probability of jumping from rank r to some higher rank r’, including a fascinating invariance property where the expected upward jump in the fitness ranking is the same no matter where we are in the ranking.  Namely, if the rank of the current genotype is j (i.e., j – 1 genotypes are better), we will jump to rank (j + 2)/4.

That’s fascinating, but what are we going to do with that information?  I suspect the idea of a fitness rank previously appeared nowhere in the history of experimental biology, because rank isn’t a measurement one takes anywhere other than the racetrack.  But remember that we would like a theory for an adaptive walk, not just 1-step adaptation.  If we jump from j to k = (j + 2)/4, then from k to m = (k + 2)/4, and so on, we could develop a theory for the trajectory of fitness increases during an adaptive walk, and for the length of an adaptive walk— for how many steps we are likely to take before we can’t climb anymore.

Figure 5.3 from Gillespie’s 1991 book. Each iteration has a number-line showing the higher-fitness genotypes accessible on the evolutionary horizon (fitness increases going to the right). At iteration #1, there are 4 more-fit genotypes. In the final iteration, there are no more-fit genotypes accessible, but there is a non-accessible more-fit genotype that was accessible at iteration #2.

The barrier to solving that theory is solving the evolutionary horizon problem.  Every time we take a step, the horizon shifts— some points disappear from view, and others appear (Figure).  We might be the 15th most-fit genotype, but at any step, only a subset of the 14 better genotypes will be accessible, and this subset changes with each step: this condition is precisely what Gillespie (1984) means by the phrase “the mutational landscape” (see Figure).  In his 1983 paper, he just assumes that all the higher-fitness mutants are accessible throughout the walk.  Gillespie’s 1984 paper entitled “Molecular Evolution over the Mutational Landscape” tackles the changing horizon explicitly.  He doesn’t solve it analytically, but uses simulations.  I won’t explain his approach, which I don’t fully understand.  Analytical solutions appeared in later work by Jain and Seetharaman, 2011 (thanks to Dave McCandlish for pointing this out).

The third and fourth key innovations are to (3) ignore differences in u and (4) treat the chances of evolution as a linear function of s, based on Haldane’s 2s.  In origin-fixation dynamics, the chance of a particular step is based on a simple product: rate of origin multiplied by probability of fixation.  Orr’s model relates the chances of an evolutionary step entirely to the probability of fixation, assuming that u is uniform. Then, using 2s for the probability of fixation means that the chance of picking a mutant with fitness si is simply si / sum(s) where the sum is over all mutants (the factor of 2 cancels out because its the same for every mutant).  Then, by applying EVT to the distribution of s, the model allows predictions based solely on the current rank.

A test of the mutational landscape model?

As noted earlier, this post started as a rant about a study that was mis-framed as though it were some kind of validation of Orr’s model.  In fact, that study is Rokyta, et al., described above.  Indeed, Rokyta, et al.  tested Orr’s predictions, as shown in the left-most panel in the figure below.  The predictions (grey bars) decrease smoothly because they are based, not on the actual measured fitness values shown above, but merely on the ranking.  The starting genotype is ranked #10, and all the predictions of Orr’s model follow from that single fact, which is what makes the model cool!

Rokyta_fig2

(Figure 2 of Rokyta, et al. A: fit of data to Orr’s model. B: fit of data to an origin-fixation model using non-uniform mutation rates. C: fit of data to origin-fixation model with non-uniform mutation and probability of fixation adjusted to fit phage biology more precisely. The right model is significantly better than the left model.)

If they did a test, what’s my objection?  Yes, Rokyta, et al. turned the crank on Orr’s model and got predictions out, and did a goodness-of-fit test comparing observations to predictions.  But, to test the mutational landscape model properly, you have to turn the crank at least 2 full turns to get the mojo working.  Remember, what Gillespie means by “evolution over the mutational landscape” is literally the way evolution navigates the change in accessibility of higher-fitness genotypes due to the shifting evolutionary horizon.  That doesn’t come into play in 1-step adaptation.  You have to take at least 2 steps.  Claiming to test the mutational landscape model with data on 1-step adaptation is like claiming to test a new model for long-range weather predictions using data from only 1 day.

The second problem is that Rokyta, et al respond to the relatively poor fit of Orr’s model by successively discarding every unique feature.  The next thing to go was the assumption of uniform mutation.  As I noted earlier, there are strong mutation biases at work.  So, in the middle panel of the figure above, they present a prediction that depends on EVT and assumes Haldane’s 2s, but rejects the uniform mutation rate.  In their best model (right panel) they have discarded all 4 assumptions.  They have measured the fitnesses (Table 1, above), and they aren’t a great fit to an exponential, so they just use these instead of the theory.  Haldane’s 2s only works for small values of s like 0.01 or 0.003, but the actual measured fitnesses go from 0.11 to 0.39!  Rokyta, et al provide a more appropriate probability of fixation developed by theoretician Lindi Wahl that also takes into account the context of phage (burst-based) replication.  To summarize,

Assumption 1 of the MLM.  The exponential distribution of fitness among the top-ranked genotypes is tested, but not tested critically, because the data are not sufficient to distinguish different distributions.

Assumption 2 of the MLM.  Gillespie’s “mutational landscape” strategy— his model for how the changing horizon cuts off previous choices and offers a new set of choices at each step— isn’t tested because Rokyta’s study is of 1-step walks.

Assumption 3 of the MLM.  The assumption that the probability of a step is not dependent on u, on the grounds that u is uniform or inconsequential, is rejected, because u is non-uniform and consequential.

Assumption 4 of the MLM. The assumption that we can rely on Haldane’s 2s is rejected, for 2 different reasons explained earlier.

Conclusion

I’m not objecting so much to what Rokyta, et al wrote, and I’m certainly not objecting to what they did— it’s a fine study, and one that advanced the field.  I’m mainly objecting to the way this study is cited by pretty much everyone else in the field, as though it were a critical test that validates Orr’s approach.  That just isn’t supported by the results.  You can’t really test the mutational landscape model with 1-step walks.  Furthermore, the results of Rokyta, et al led them away from  the unique assumptions of the model.  Their revised model just applies origin-fixation dynamics in a realistic way suited to their experimental system— which has strong mutation biases and special fixation dynamics— and without any of the innovations that Orr and Gillespie reference when they refer to “the mutational landscape model.”

Constructive neutral evolution on Sandwalk

September 11, 2015 / Arlin Stoltzfus / 3 Comments

The interesting things at Sandwalk always seem to happen when I’m not looking.  On Sunday, while I was out west taking the offspring to start university at UBC, Larry Moran posted a blog on Constructive Neutral Evolution that has elicited almost 200 comments.  Alas, many of the comments are not particularly useful, as Sandwalk is home to an ongoing pseudoscientific debate on intelligent design.

The one point that I would like to make about CNE is that it was not proposed as some kind of law or tendency (i.e., not like “Biology’s First Law” of McShea and Brandon).  Some other people treat CNE as the manifestation or the realization of some kind of intrinsic tendency to complexification. If this were the case, then examples of reductive evolution (e.g., cases involving viruses and intracellular parasites) would raise a question about the generality of the idea.  Obviously evolutionary change occurs in both reductive and constructive modes.  Bateson and Haldane each speculated that reductive evolution would be common because it is so easy to accomplish.

From my perspective, CNE is not a theory about a general tendency of evolution.  Instead it is a schema for generating specific testable hypotheses of local complexification.

One also can imagine a mode of Reductive Neutral Evolution in which simplification occurs. It is simply a matter of the local position of the system relative to the spectrum of mutational possibilities.

 

The surprising case of origin-fixation models

October 23, 2014 / Arlin Stoltzfus / 3 Comments

In a recent QRB paper with David McCandlish, we review the form, origins, uses, and implications of models (e.g., the familiar K = 4Nus) that represent evolutionary change as a 2-step process of (1) the introduction of a new allele by mutation, followed by (2) its fixation or loss.

What could be surprising about these “origin-fixation” models, which are invoked in theoretical models of adaptation (e.g., the mutational landscape model) and in widely used methods applied to phylogenetic inference, comparative genomics, detecting selection, modeling codon usage, and so on?

Quite a lot, it turns out. (more…)

The Great Non-Debate on Evolutionary Theory (Nature, Oct 2014)

October 17, 2014 / Arlin Stoltzfus / 5 Comments

Some of you may have noticed a recent exchange in Nature on the question of whether evolutionary biology needs a re-think. The online article does not make clear the alignments of the listed authors, but those arguing in favor of a re-think are:

  • Kevin Laland, Tobias Uller, Marc Feldman, Kim Sterelny, Gerd B. Müller, Armin Moczek, Eva Jablonka, and John Odling-Smee

and those arguing against are:

  • Gregory A. Wray, Hopi E. Hoekstra, Douglas J. Futuyma, Richard E. Lenski, Trudy F. C. Mackay, Dolph Schluter and Joan E. Strassmann

I was a bit surprised that they didn’t get people who actually disagree about science, like Mike Lynch and Sean Carroll.  Instead, the debate takes place between participants who disagree on the meta-scientific question of whether the field needs a re-think.  What is each side saying?
(more…)

Theory vs. Theory

October 14, 2014 / Arlin Stoltzfus / 0 Comments

What does it mean to invoke “evolutionary theory”? Is “neo-Darwinism” (or “Darwinism”) a theory, a school of thought, or something else? What gives a theory structure and meaning?  Can a theory change and, if so, how much?  What is the relationship between mathematical formalisms and other statements of “theory”? Who decides how a theory is defined, or redefined (e.g., is Ohta’s “nearly neutral” theory an alternative to, or a variant of, Kimura’s Neutral Theory of Molecular Evolution)?

For various purposes, it is useful to have a framework for discussing “theory” and “theories”.  Here I begin by identifying two distinct ways that scientists use the word “theory”. 1
(more…)