Bad takes #7: requires sign epistasis
Unfamiliar ideas are often mis-identified and mis-characterized. It takes time for a new idea to be sufficiently familiar that it can be debated meaningfully. We look forward to those more meaningful debates. Until then, fending off bad takes is the order of the day! See the Bad Takes Index.
Svensson (here or here) has repeatedly asserted that the effect of biases in the introduction process requires reciprocal sign epistasis, with the implication that this makes the effect unlikely in nature.
Epistasis is inescapably relevant when considering extended adaptive walks on realistic fitness landscapes, but sign epistasis is certainly not a requirement for effects of biases in the introduction process. This is an invention of Svensson, not listed as a requirement in any of the published works of scientists developing theory on this topic. For instance, Rokyta, et al. (2005) have no epistasis in their model of 1-step adaptation. Gomez, et al. (2020) present a staircase model of fitness without sign epistasis.
In some cases, the fitness landscape is specified by an empirical model, e.g., the “arrival of the frequent” model of Schaper and Louis (2014) simply uses the genotype-phenotype map for RNA folds that emerges from RNA folding algorithms. Cano and Payne (2020) use empirical fitness landscapes of transcription-factor binding sites, which typically have a small number of peaks. Whatever the degree of epistasis found on these landscape, it is the naturally occurring degree for this kind of landscape.
The superficial plausibility of Svensson’s fabrication arises from the fact that reciprocal sign epistasis is indeed a feature of the original computer simulations of Yampolsky and Stoltzfus (2001). Why is this feature present?
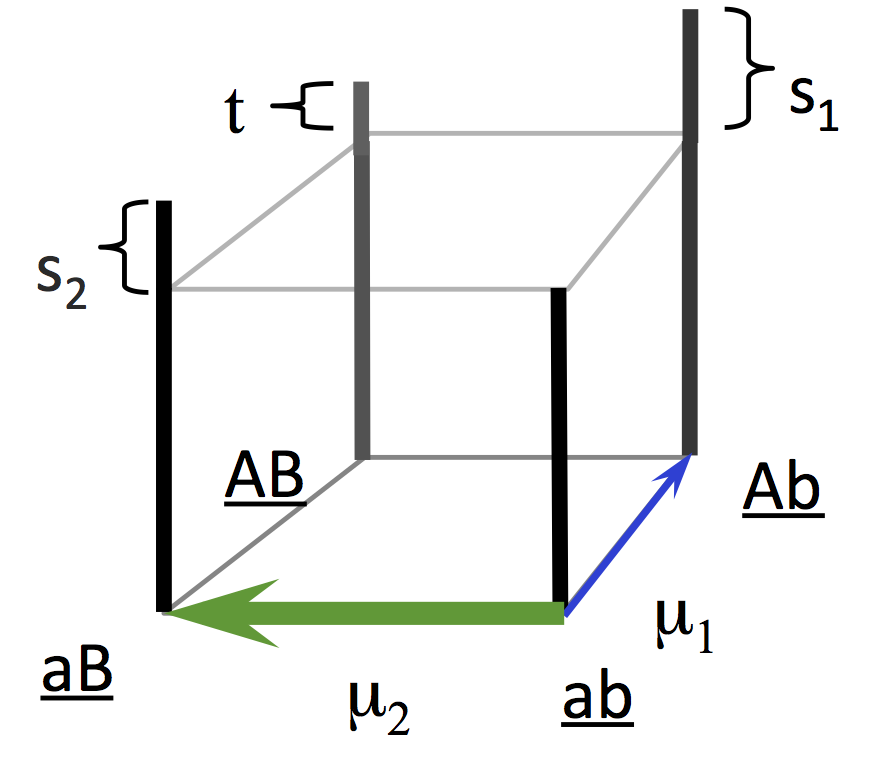
In the original model, the initial ab population can evolve either to Ab or to aB, but further evolution to AB does not occur because AB is less fit (i.e., in the figure, t is less than s1 or s2). This means that the change from a to A is beneficial in the b background, but deleterious in the B background. When one allelic substitution reverses the effect of another, this is called sign epistasis, and when the effect goes both ways, that is reciprocal sign epistasis.
Remember, the Yampolsky-Stoltzfus model was designed to be the simplest model to prove a point, so it is a model of one-step adaptation with two options: up and to the left, or up and to the right. Thus, we could have avoided sign epistasis by stipulating that the left and right options are mutually exclusive, e.g., we could have stipulated that the initial population has T at a specific nucleotide site, and that the left and right options are C (transition) and A (transversion). The behavior of such a model would be almost identical to the original. Or we could have stipulated (1) an infinite landscape where each derived genotype has a similar left-right choice with no epistasis, but (2) we are only going to look at the first step.
More generally, the way to understand this issue more deeply is to contrast two kinds of scenarios: (1) the idealistic scenario in which the evolving system proceeds to the fitness optimum at equilibrium, in infinite time, so that biases in introduction have no final effect, and (2) everything else, i.e., non-idealistic scenarios in which multiple outcomes are possible, and the choice might reflect biases in the introduction of variation.
Many conditions lead to models of the second type, i.e., realistic models (for a larger discussion, see here). For instance, ending evolution with the first beneficial change is the actual model used recently by Cano, et al. (2021), and it corresponds to the natural scenario of antibiotic resistance evolution explored empirically by Payne, et al. (2019). Resistant M. tuberculosis isolates emerge, and they are isolated and analyzed, without waiting for some long-term process of adaptive optimization to take place. They are isolated and analyzed by virtue of having evolved resistance, not by virtue of having reached a global fitness optimum for resistance.
More generally, we could stipulate that the space is large compared to the amount of time to explore it, so that kinetic biases influencing the early steps are important. In the antibiotic resistance scenario, one is literally looking at the first step in evolution, because that is the step that counts. For instance, one could simply posit an infinite space and compare the rates of two origin-fixation processes that differ due to a mutation bias, e.g., GC-increasing or GC-decreasing changes in an infinitely long genome. No sign epistasis is required, and the effect would apply even given completely additive effects.
In a more finite model in which the system has time to explore the landscape of possibilities, sign epistasis, diminishing-returns epistasis, and other kinds of frustration can have the effect of locking in consequences of initial steps that are subject to kinetic biases. Such effects are common for protein-coding regions because, from a given starting codon for 1 type of amino acid, only 4 to 7 other amino acids — not all 19 alternatives — are accessible by a single-nucleotide mutation. Thus, even when the effects of amino acid changes are all additive, the landscape is rough for a protein-coding gene evolving by single-nucleotide mutations, so that biases in the introduction process can influence the final state of the system. This effect is evident in the theoretical study by Stoltzfus (2006).
In summary, the true relevance of sign epistasis to understanding the efficacy of biases in the introduction process is roughly as follows. When you haven’t got far from where you started, your path depends a lot on your first steps. So, kinetic biases reflecting what is mutationally likely are going to be relevant to understanding the path of an evolving system when the amount of change is non-large relative to the size of the space to be explored. When evolution has plenty of time to explore a small finite landscape, as in the Yampolsky-Stoltzfus model, we can still see consequences of kinetic bias in the case where epistasis has the effect of locking in these consequences.