When “Darwinian adaptation” is neither
Getting stuff right
Early in the evolution of the Sequence Ontology, it was noted (by gadflies like myself) that SO asserts the relationship of mRNA to gene to be the “part of” relationship. This is obviously wrong. An RNA molecule is not part of a DNA molecule. Saying that mRNA is part of a gene is like saying that a CD with some audio chapters from a book is part of that book.
Ontologies are supposed to support formal reasoning: errors in representation will lead inevitably to erroneous results. For instance, if we are reasoning about the chemical composition of a cell using mRNA part_of gene as a constraint, we would conclude falsely that the mass of DNA must always be at least as much as the mass of mRNA, because the mass of a thing is always at least as great as the mass of some specified parts.
Though SO developers later chose to avoid part_of, they still warn us explicitly that SO is a kind of mapping language designed for the purpose of genome annotation, which can lead to problems if used in other contexts.[1] In the annotation context, an annotated mRNA region is part of a gene region, in the sense that the projection of the encoded part of the mRNA onto the genome is part of the gene (this also applies to my analogy of the audio CD).
The point of this is that it is important to get stuff right. That should be obvious. When we say in the context of formal reasoning that X has the part_of relation to Y, it ought to mean that X is part of Y. With this in mind, I want to call attention to the tendency to refer to certain contemporary mutation-driven models as models of “Darwinian adaptation” or “Darwinian evolution” (e.g, here or here). This suggests that little has changed in 150 years, and that contemporary science merely fulfills Darwin’s vision.
Nothing could be further from the truth.
Models like the mutational landscape model correspond, not to what Darwin and his Modern Synthesis followers believed about how evolution works, but to what their most important opponents believed. Darwin’s “neo-Darwinian” followers would have rejected the mutational landscape model as being neither neo-Darwinian nor a model of adaptation.
The mutational landscape model
To understand this difference, let’s begin with the MLM (mutational landscape model), which has been at the center of a minor renaissance in evolutionary genetics. The MLM is based on several key assumptions. The first is that evolution proceeds by discrete steps in a discrete “genotype space”, a valuable idea used in many models of evolution (not just MLM), illustrated in this lovely figure by Stadler and Stephens.
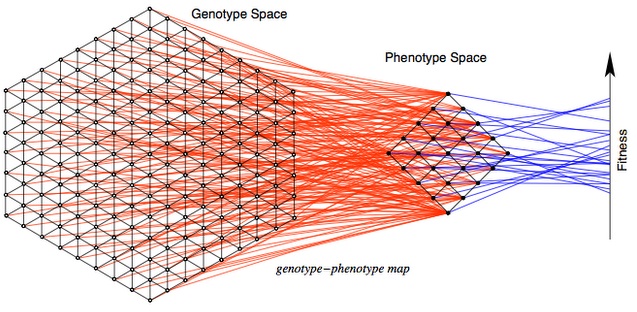
The second assumption is that allowable steps are restricted to some set of mutational neighbors, e.g., a DNA sequence of N nucleotides has 3N neighbors accessible by a single nucleotide substitution mutation. In the model, evolution explores only this local landscape, which changes with each mutational step. This is an enormously useful simplification! We don’t have to consider an astronomically large number of possible genotypes, but only the mutationally accessible neighborhood.
The next key assumption is that the evolving system is already well adapted, so that further beneficial changes represent the extreme upper tail of a distribution of fitnesses. This allows one to invoke extreme value theory to make generalizations about the interval from one beneficial genotype to the next.
So far, we have specified the set of accessible states, and a theory for the distribution of their fitnesses. I’m not sure why any of this is called a “landscape”, IMHO an over-used metaphor. For me, a better metaphor is an “evolutionary horizon” (because the horizon is as far as you can see, and it changes with each step). When Gillespie invoked the “mutational landscape”, he meant to draw attention to the way in which the distribution of accessible alternatives changes with each step (for a more advanced explanation of this model, see Understanding the Mutational Landscape Model).
Finally, we need a “move-rule” for going from the current state to a more fit state. The MLM move-rule is based on origin-fixation dynamics, i.e., treating evolution as a 2-step process of the origination of a new allele by mutation, and its subsequent fixation or loss [2]. As we are concerned only with beneficial changes, we can use Haldane’s approximation that the chance of fixation of a new beneficial allele is 2s, twice the selection coefficient. Given this, and assuming that all mutation rates are the same, as in Orr (2002), we end with a very simple expression for the chance that the next step is to genotype j:
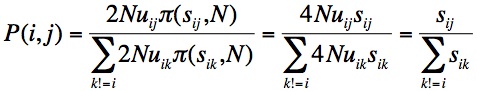
That is, starting from allele i, the chance of moving to j is simply the selection coefficient sij relative to the sum of all selection coefficients sik, where k != i. To implement this in a computer program, we just make a number line with the s values for each beneficial neighbor, then pick randomly from the number line to choose the next genotype (then recompute the neighborhood in preparation for the next step).
Putting all of this together, we get a model of stepwise evolution that allows substantive predictions about the dynamics of change in fitness. This is marvelous, and a true innovation!
But is it Darwinian adaptation?
Classically, the process of adaptation is conceived as a stimulus-response dynamic: conditions change, then a biotic system adjusts, representing either short-term (physiological) or long-term (evolutionary) adaptation. Colloquial usage has the same connotation: when we admire someone’s adaptability, we mean that they respond in a graduated way to changes in conditions, not that they suddenly have a great new idea, nor that they continually improve in a constant environment.
We do not have a widely used term in evolutionary biology for aptation, the process by which the aptness of a species increases without a change in conditions. Over time, we have come to use the term “adaptation” to cover both adaptation proper, and mutation-initiated aptation.
But it was not always this way. Shull’s 1936 textbook Evolution (an example of a pre-Synthesis textbook) states, in regard to mutation-initiated aptation, “the whole process as Goldschmidt conceives it is one that was sponsored by Cuenot and Davenport and by the former called preadaptation. First a change occurred, fitting individuals for a new situation, and then sometimes the new situation was either near at hand or was accidentally reached” (p. 254, my emphasis). Note that Shull implicates 3 other scientists associated with historical mutationism: Charles Davenport, Lucien Cuénot, and Richard Goldschmidt. When Cavalli-Sforza and Lederberg (1956) set out to show that mutations conferring antibiotic resistance are spontaneous in the sense of appearing prior to selection, their paper was entitled “Isolation of Pre-Adaptive Mutants in Bacteria by Sib Selection,” and the paper referred to the preadaptation theory.
Similarly, the architects of the Modern Synthesis distinguished adaptation proper (envisioned as a smooth programmatic response to an external stimulus) from a process they call “pre-adaptation” or “random pre-adaptation” in which the character of the adaptation is in some sense pre-determined by a particular mutation that happens to arise (p. 157, 236, 257 of Simpson 1967; p. 121 of Mayr 1963). Referring to early geneticists, Simpson complained that “the problem of adaptation was, in their opinion, solved abolishing it: they proclaimed that there is no adaptation, only random pre-adaptation.” Dobzhansky (1974, p. 325) gives the example of DDT resistance in insects, arguing that resistant flies must have been present in the population prior to exposure, which makes the process something different than a responsive adjustment, something he also calls “preadaptation.”
We have lost the language for this distinction, but the distinction has not entirely disappeared, e.g., Hermisson, et al. (2005) begin by defining adaptation in classic fashion as a process initiated by a change in conditions (“environmental change or the colonization of a new niche”), then present, as alternative models for this process, both the classic model based on standing variation and the “new mutations” model— even though the latter model depicts change initiated by a mutation and therefore is not “adaptation” as they define it. The authors complain that the new mutations model is widely assumed by molecular evolutionists, while the classical view suffers from “conspicuous neglect”. Actually, if you read Orr’s presentation of the mutational landscape model carefully, he begins by stating that a change in conditions occurs (although this plays no direct role in the model).
Mutationism and the origin-fixation view
As should be apparent by now, this is not merely a semantic distinction, but refers to a substantive difference in views of how evolution works. We could even call it a historic line of battle: early geneticists such as de Vries, Punnett, Morgan, Davenport, et al. often conceived of evolutionary change as mutation-initiated aptation, whereas Mayr, Dobzhansky, Simpson et al typically dismissed or disparaged this view as evolution by “lucky mutations.”
This difference is masked oddly in Orr’s (2005) account of the history of models of adaptation. Fisher’s famous “geometric model” justified infinitesimalism by arguing that the smallest changes were the most likely to be beneficial, thus evolutionary change would be based on such infinitesimal effects. Decades later, Kimura invoked Fisher’s geometric model, yet appealed to the probability of fixation, which increases with the size of effect, leading to a different conclusion, namely that intermediate (not infinitesimal) effects were the most likely, because they have the highest joint probability of being beneficial and being fixed.
In explaining this development, Orr says that “Fisher’s interpretation was confused”, and that Kimura corrected it.
No, actually. Fisher simply had a different understanding of evolution than Kimura (and Orr). Origin-fixation models were not invented until 1969 (by King & Jukes, and Kimura & Maruyama: see McCandlish and Stoltzfus, 2014). The architects of the Modern Synthesis were committed to a “shifting gene frequencies” view in which selection never waits for a new mutation, and “evolution” is a shift from one multi-locus distribution of allele frequencies to another, without new mutations. The writings of the Modern Synthesis are rich in statements (see McCandlish and Stoltzfus or The Shift to Mutationism is Documented in Our Language) that reject the origin-fixation view, even before it was formalized in 1969: when they were arguing for their distinctive “shifting gene frequencies” view throughout the 1960s and 1970s, they were arguing against both (1) the earlier Mendelian-mutationist view (Stoltzfus and Cable, 2014) and (2) the emerging “molecular evolution” view.
That is, Kimura fundamentally changed Fisher’s argument by placing it in the context of an origin-fixation theory that Fisher would have rejected.[3] To understand Fisher’s view, begin with a gene pool in equilibrium. The environment changes, and this results in fitnesses being reassigned to alleles. The ones that become beneficial will increase in frequency deterministically until a global optimum is reached. The deleterious ones will fall to their deterministic mutation-selection balance frequencies. All Fisher needs to know is the chance of being beneficial as a function of size. His geometric argument answers this question. Fisher’s argument is complete, given his view of evolution.
Darwin, likewise, rejected the idea that adaptation occurs by mutational jumps. In his theory based on blending of masses of individually trivial variations, a mutant individual cannot be the start of something new in evolution; selection cannot act on a singular difference meaningfully because hereditary substances are inconstant [4]. Darwin’s critics often misunderstood this aspect of his theory. When challenged with the criticism that his theory was “not a theory of the Origin of Species at all, but only a theory on the causes which lead to the relative success and failure of such new forms as may be born into the world”, Darwin’s response was: “that may be a very good theory, but it is not mine” (p. 45 of Poulton, 1909, 50 Years of Darwinism).
Getting theories right
Thus, referring to the mutational landscape model as a model of “Darwinian evolution” or “Darwinian adaptation” is problematic. We should hesitate to call this “adaptation” because it is not a model of a response to environmental change. But more importantly, we should hesitate to use the label “Darwinian”.
If we mean to implicate a high-level theory such as Darwinism, mutationism, Lamarckism, etc., then the proper way to describe the MLM and similar models is to say that they represent de Vriesian [5] or mutationist adaptation (or aptation), corresponding to a view of evolution that Darwin and his followers clearly disavowed, and that is clearly labeled in historical sources as non-Darwinian or anti-Darwinian.
Might “Darwinian” mean something else in this context? One often sees the phrase “Darwinian positive selection” or “positive Darwinian selection” in the literature, as distinct from “negative selection.” Why not just “positive selection”? Is there some other, non-Darwinian kind of positive selection? Is this an attempt to distinguish “Darwinian selection” from other kinds of selection? If so, this is again problematic. As historian Jean Gayon points out in Darwinism’s Struggle for Survival, “the Mendelians [i.e., the mutationists or early geneticists] were responsible for the operational definition of natural selection that is most widely used today— the diffusion of a gene in a population” (p. 181). Darwin’s 19th-century conception of natural selection was not a Mendelian rate of allele replacement, and certainly not a stochastic filter.
In summary, when evolutionary geneticists refer to the mutational landscape model as “Darwinian adaptation”, or when Dean (2012) refers to “random mutation” and “the sieve of natural selection” as “basic Darwinian principles”, this is an example of getting things wrong. It distorts history, and rewards Darwin and his followers with scientific credit that rightfully belongs to others.
More importantly for the sake of scientific inquiry, it is a missed opportunity to reflect on why Darwin and his followers were so eager to reject a lucky mutant view of evolution that we now accept as logically obvious and probably important. Evidently there was something important at stake. Think about it. Why do scientists stake out a position on something, before facts have resolved the issue?
References cited
Dean AM. 2012. Evolution: a View from the 21st Century. Microbe Magazine.
Dobzhansky T. 1974. Chance and Creativity in Evolution. In: Ayala F, Dobzhansky T, editors. Studies in the Philosophy of Biology: Reduction and Related Problems. Berkeley and Los Angeles: University of California Press. p. 307-338.
Mayr E. 1963. Animal Species and Evolution. Cambridge, Massachusetts: Harvard University Press.
Orr HA. 2002. The population genetics of adaptation: the adaptation of DNA sequences. Evolution Int J Org Evolution 56: 1317-1330.
Shull AF. 1936. Evolution. New York: McGraw-Hill.
Simpson GG. 1967. The Meaning of Evolution. New Haven, Conn.: Yale University Press.
Stadler PF and CR Stephens, Landscapes and Effective Fitness, reprint available via ResearchGate
Notes
[1] In the current SO, the part_of relation is replaced by a member_of relation (click to view the mRNA concept in SO). By way of explaining the task-specificity of SO, Mungall, et al, write
Genome annotations specify the coordinates of sequence features that are manifest in one or more of the kinds of molecule defined by the central dogma. For example, although an intron is manifest as an RNA molecule, the coordinates of the intron can be projected onto the genomic sequence. The term labels chosen for SO were those in use by the genome annotation community, thus “transcript”, “intron” and so on were chosen as labels for the sequence feature types corresponding to genome regions encoding actual transcript and intron molecules. This polysemy does not cause problems when SO is used purely for genome annotation, but is potentially confusing when it is used in the context of other ontologies.
This is amusing for those of us who have watched the biological ontology enterprise with dismay as the inner circle of OBO insisted that ontologies represent The Truth About Reality— which quite conveniently for OBO is covered by ancient Greek philosophy—, while disparaging the attitude that ontologies are heuristic tools. All of this was done while embracing ontologies such as SO or GO that are clearly heuristic, merely because GO is the most widely used ontology in the known universe and one can’t claim to be the go-to organization for biological ontologies without including GO.
[2] See McCandlish and Stoltzfus for a fuller explanation. The rate of evolution K in an origin-fixation model is the rate of introduction, 2N*u, multiplied by the probability of fixation. Using 2s as the probability of fixation, we get K=4Nus for each type of change. Because the waiting time is exponential with mean 1/K, the chance that we’ll see genotype j next, instead of k, is just the ratio of rates. In the equation shown, the probability that j is the next step is just the rate of going to j relative to the sum of rates of going to all possible changes.
[3] Interestingly, Wright (1938) developed a model whose behavior clearly converges on origin-fixation dynamics, though it is not structurally an origin-fixation model. At the end of the paper, Wright described this behavior, not as adaptation, but as evolution determined by “mutation pressure”. His comments on the model are bewildering. He seems to think of it merely as a model of the degeneration of characters.
[4] That is, we cannot assign a selection coefficient to a hereditary factor in Darwin’s view, because hereditary substances are not discrete constant factors. The character and potency of the hereditary substances change in response to conditions, and these substances blend during reproduction.
[5] de Vries is surely not the first source for this way of thinking, though he may be the best. Many readers simply misinterpreted Darwin as though he had proposed a theory of lucky mutations.


Comments